www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Aplikasi Integral › Luas Antara Dua Kurva
Luas Antara Dua Kurva
Luas daerah yang berada di atas atau di bawah sumbu-x dapat dicari dengan mudah karena kita bisa menuliskan integral dengan mudah. Akan tetapi, bagaimana mencari luas daerah yang berada di antara dua kurva?
Sebelumnya kita telah membahas cara menghitung luas daerah yang berada di atas dan di bawah sumbu x dari suatu fungsi \(f(x)\). Sekarang kita akan lanjutkan ke luas daerah yang berada di antara dua kurva.
Contoh-contoh yang diberikan dalam menghitung luas untuk daerah yang berada di atas maupun di bawah sumbu-x dapat dengan cepat kita kerjakan karena kita bisa menuliskan integral dengan mudah. Akan tetapi, kadang kita akan menjumpai soal yang lebih rumit, misalnya ketika kita mencari luas daerah yang berada di antara dua kurva.
Hal ini menjadi rumit karena kita sulit menentukan pemilihan integral yang benar. Tetapi, terdapat suatu cara berpikir yang dapat sangat membantu. Berikut adalah cara berpikir tersebut dalam lima langkah.
Langkah 1. Gambarlah daerah yang bersangkutan
Langkah 2. Potonglah menjadi jalur-jalur dan berilah nomor pada suatu jalur tertentu.
Langkah 3. Hampiri luas suatu jalur tertentu tersebut dengan luas persegi panjang yang sesuai.
Langkah 4. Jumlahkah luas aproksimasi tersebut.
Langkah 5. Kemudian ambillah limit dari jumlah itu dengan cara menunjukkan panjang jalur ke nol sehingga diperoleh suatu integral tertentu.
Untuk menjelaskan apa yang dimaksudkan di atas, perhatikanlah contoh sederhana berikut ini.
CONTOH 1:
Susunlah integral untuk luas daerah di bawah kurva \(y=1+\sqrt{x}\) yang terletak antara garis \(x = 0\) dan \(x = 4\) (Gambar 1).

Gambar 1.
Setelah kita pahami dengan benar prosedur lima langkah tersebut, kita dapat menyingkatnya menjadi tiga langkah, yaitu: potong-potong (slice), aproksimasikan, dan integralkan.
Ingatlah bahwa mengintegralkan berarti, menjumlahkan dan mengambil limit apabila panjang jalur menuju nol. Dalam proses ini \(∑… Δx\) berubah menjadi \(∫… dx\). Gambar 2 menunjukkan proses yang telah dipersingkat itu untuk soal yang sama.
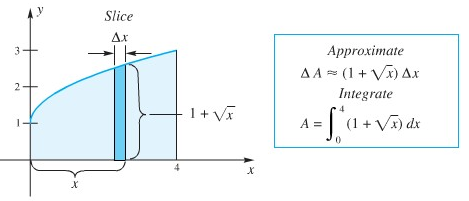
Gambar 2
Setelah prosedur-prosedur di atas dipahami, sekarang kita siap menghitung luas daerah yang berada di antara dua kurva. Tinjaulah kurva-kurva \(y=f(x)\) dan \(y=g(x)\) dengan \(g(x)≤f(x)\) pada selang \(a≤x≤b\). Kurva-kurva dan selang yang diberikan membatasi daerah yang tergambar pada Gambar 3. Kita akan gunakan tiga prosedur: potong, aproksimasi, integralkan, untuk menentukan luas daerah tersebut.

Gambar 3
CONTOH 2:
Tentukan luas daerah antara kurva \(y=x^4\) dan \(y=2x-x^2\).
Pembahasan:
Kita mulai dengan menentukan titik-titik potong kurva-kurva tersebut dan kemudian menggambarkannya. Kita perlu mencari akar-akar persamaan \(2x-x^2=x^4\), suatu persamaan berderajat empat, yang biasanya tidak mudah terpecahkan. Akan tetapi, tampak bahwa \(x = 0\) dan \(x = 1\), adalah dua di antara akar-akarnya. Gambar daerah, potongan jalur dan aproksimasi, serta integral yang bersangkutan dapat dilihat pada Gambar 4 berikut.
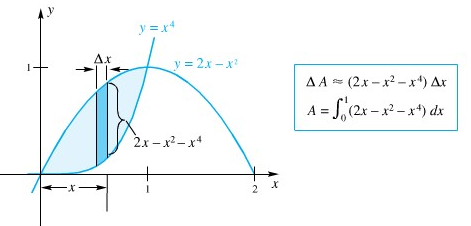
Gambar 4
Dengan menghitung integral tersebut, kita akan peroleh luas yang ada di antara dua kurva tersebut.
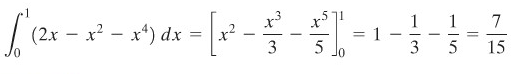
CONTOH 3:
Tentukan luas daerah yang dibatasi oleh parabol \(y^2=4x\) dan garis \(4x-3y=4\).
Pembahasan:
Tuliskan kembali persamaan kedua menjadi \( 4x = 3y+4 \), kemudian kita tentukan titik potong parabol dan garis koordinat y.

Dengan demikian, titik-titik potong tersebut adalah (4,4) dan (1/4,-1). Daerah yang harus dicari luasnya dapat dilihat pada Gambar 5.

Gambar 5.
Daerah ini kita potong-potong menjadi jalur-jalur tegak (vertikal), seperti terlihat pada gambar. Ada kesulitan sedikit, karena kurva batas bawah terdiri atas dua kurva. Di sebelah kiri sekali jalur-jalur merentang dari bagian bawah parabol hingga bagian atasnya, sedangkan untuk daerah sisanya jalur-jalur ini merentang dari garis hingga parabol. Jadi, apabila kita menggunakan jalur-jalur tegak, kita perlu membagi daerah yang bersangkutan menjadi dua bagian, kemudian membentuk integral untuk masing-masing bagian; kemudian menghitungnya.
Tentu saja membagi daerah menjadi dua bagian, dan kemudian menghitungnya terasa agak rumit. Suatu penyelesaian yang jauh lebih sederhana ialah memotong daerah menjadi jalur-jalur yang datar, seperti dapat kita lihat pada Gambar 6. Dalam hal ini kita menggunakan \(y\) sebagai variabel dalam integral, dan bukan \(x\). Perhatikan bahwa jalur-jalur yang datar itu selalu bermula pada parabol (di sebelah kiri) dan berakhir pada garis (di sebelah kanan).

Gambar 6.
Dengan demikian, berdasarkan Gambar 6, luas daerah tersebut dapat dihitung sebagai berikut.

Ada dua hal yang harus diperhatikan, yaitu (1) integran yang menyangkut penjaluran datar mengandung variabel \(y\), bukan \(x\); dan (2) untuk memperoleh integran, kita nyatakan x sebagai fungsi \(y\) dari dua persamaan yang diketahui. Kemudian kita kurangkan nilai \(x\) yang lebih kecil (kurva kiri) dari nilai \(x\) yang lebih besar (kurva kanan).
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Seseorang yang pernah melakukan kesalahan dan tidak pernah memperbaikinya berarti Ia telah melakukan satu kesalahan lagi.
