Kalkulus I   »   Fungsi   ›  Domain dan Range Fungsi

Domain dan Range Fungsi

Jika x dan y terkait oleh persamaan y = f(x), maka himpunan semua input atau nilai x yang diperbolehkan disebut domain dari fungsi f(x), dan himpunan output atau nilai y yang dihasilkan untuk setiap x dalam domain disebut daerah hasil atau range dari f(x).

Fungsi merupakan objek penting dalam kalkulus karena mereka menggambarkan dunia riil dalam bentuk matematika. Untuk memberi nama fungsi dipakai sebuah huruf tunggal seperti \(f\) (atau \(g\) atau \(F\)).

Dengan demikian \(f(x)\), yang dibaca “\(f\) dari \(x\)” atau “\(f\) pada \(x\)”, menunjukkan nilai yang diberikan oleh \(f\) kepada \(x\). Jadi, jika \(f(x)=x^3-4\), maka

Pemahaman yang jelas tentang cara menuliskan fungsi adalah hal yang sangat penting dalam kalkulus. Sekarang mari kita beralih ke istilah lain yang juga penting terkait fungsi yakni daerah asal (domain) dan daerah hasil (range).

Jika \(x\) dan \(y\) terkait oleh persamaan \(y = f (x)\), maka himpunan semua input atau nilai \(x\) yang diperbolehkan disebut domain \(f(x)\), dan himpunan output atau nilai \(y\) yang dihasilkan untuk setiap \(x\) dalam domain disebut daerah hasil atau range dari \(f(x)\).

Sebagai contoh, jika \(F\) adalah suatu fungsi \(F(x)=x^2+1\) dan jika daerah asalnya dirinci sebagai \(\{-1,0,1,2,3\}\), maka daerah hasilnya adalah \(\{1,2,5,10\}\). Perhatikanlah Gambar 1 berikut ini.

Gambar 1.

Terkadang kondisi tertentu dapat memaksa pembatasan (restriction) pada nilai input yang diperbolehkan dari suatu fungsi. Misalnya, jika \(y\) menunjukkan luas suatu persegi dengan panjang sisi \(x\), maka variabel-variabel ini dihubungkan oleh persamaan \(y = x^2\). Karena panjang suatu persegi tidak mungkin negatif maka kondisi ini memaksakan diberlakukannya persyaratan bahwa \(x≥0\).

Dalam beberapa kasus kita akan menyatakan domain secara eksplisit saat mendefinisikan suatu fungsi. Misalnya, jika \(f(x)=x^2\) adalah luas persegi dengan sisi \(x\), maka kita bisa menuliskan \[ f(x)=x^2, \quad x≥0 \] untuk mengindikasikan bahwa kita mengambil domain \(f\) untuk himpunan bilangan riil tak negatif. Perhatikan gambar di bawah.

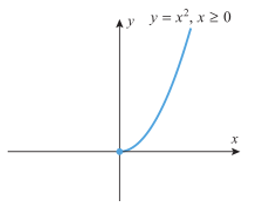
Gambar 2.

Ketika suatu fungsi didefinisikan dengan rumus matematika, rumus itu sendiri dapat memberlakukan pembatasan pada input yang diperbolehkan. Sebagai contoh, jika \(y = 1 / x\), maka \(x = 0\) bukan input yang diperbolehkan karena pembagian dengan nol tidak terdefinisi, dan jika \(y = \sqrt{x}\), maka nilai negatif \(x\) bukan input yang diperbolehkan karena akan menghasilkan nilai imajiner untuk \(y\).

Bilamana untuk sebuah fungsi daerah asalnya tidak dirinci, kita selalu menganggap bahwa daerah asalnya adalah himpunan bilangan riil sehingga aturan fungsi ada maknanya dan memberikan nilai bilangan riil. Ini disebut daerah asal mula (domain natural).

Sumber:

Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.

Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.