www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Teknik Pengintegralan › Integral Pangkat Trigonometri
Integral Pangkat Trigonometri
Apabila kita menggunakan teknik substitusi dan dibarengi dengan pemakaian kesamaan trigonometri yang tepat, maka kita dapat mengintegralkan banyak bentuk trigonometri.
Apabila kita menggunakan teknik substitusi dan dibarengi dengan pemakaian kesamaan trigonometri yang tepat, maka kita dapat mengintegralkan banyak bentuk trigonometri. Kita akan membahas lima jenis integral dengan pangkat trigonometri yang sering muncul.

Mari kita bahas satu per satu berikut ini.

Aapabila \(n\) bilangan bulat ganjil dan positif, maka kita mengeluarkan faktor \(\sin{x}\) dan \(\cos{x}\), kemudian gunakan kesamaan \(\sin^2{x}+\cos^2{x}=1\). Perhatikan contoh berikut.
CONTOH 1: \(n\) ganjil
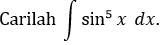
Penyelesaian:

Apabila \(n\) positif genap, kita gunakan rumus setengah sudut, yaitu

CONTOH 2: \(n\) genap
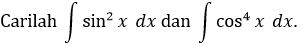
Penyelesaian:



Apabila \(m\) atau \(n\) ganjil positif sedangkan eksponen yang lain bilangan sebarang, kita keluarkan \(\sin{x}\) atau \(\cos{x}\) dan menggunakan kesamaan \(\sin^2{x}+\cos^2{x}=1\).
CONTOH 3: \(m\) atau \(n\) ganjil
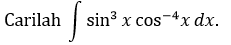
Penyelesaian:

Bila \(m\) dan \(n\) bilangan positif genap, maka kita dapat menggunakan rumus setengah sudut untuk mengurangi derajat integran.
CONTOH 4: \(m\) dan \(n\) genap

Penyelesaian:


Untuk menyelesaikan integral jenis ini kita gunakan kesamaan berikut
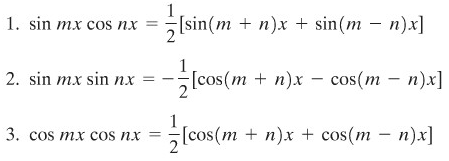
CONTOH 5:
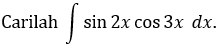
Penyelesaian:

CONTOH 6:
Jika \(m\) dan \(n\) bilangan positif buktikan bahwa

Penyelesaian:
Terapkan persamaan identitas perkalian 2 di atas. Jika \(m ≠ n\), maka

Jika \(m = n\),


Dalam kasus tangen, keluarkan faktor \(\tan^2{x}=\sec^2{x}-1\); dalam kasus kotangen, keluarkan faktor \(\cot^2{x}=\csc^2{x}-1\).
CONTOH 7:
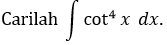
Penyelesaian:
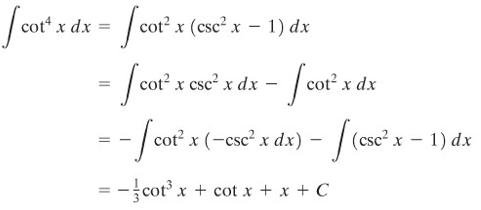
CONTOH 8:

Penyelesaian:


CONTOH 9: \(n\) genap, \(m\) sebarang

Penyelesaian:

CONTOH 10: \(m\) ganjil, \(n\) sebarang
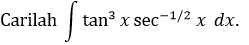
Penyelesaian:

Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Pertama kita membentuk kebiasaan dan kebiasaan akan membentuk kita. Kalahkan kebiasaan buruk Anda, atau mereka akan mengalahkan Anda.
