www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Integral › Integral tak tentu
Integral tak tentu
Dalam matematika kita akan menjumpai banyak pasangan operasi balikan (inversi); misalnya penambahan dan pengurangan, perkalian dan pembagian. Operasi balikan dari pendiferensialan disebut anti pendiferensialan atau integral tak tentu.
Dalam matematika kita akan menjumpai banyak pasangan operasi balikan (inversi); misalnya penambahan dan pengurangan, perkalian dan pembagian, pemangkatan dan penarikan akar, serta penarikan logaritma dan penghitungan logaritma.
Kita telah membahas pendiferensialan (penurunan); dan sekarang kita akan membahas balikannya yang disebut anti pendiferensialan (antiturunan) atau integral tak tentu.
Perhatikan definisi untuk anti turunan berikut ini.
DEFINISI:
Kita sebut \(F\) suatu antiturunan \(f\) pada selang \(I\) jika \(D_x F(x)=f(x)\) pada \(I\), yakni, jika \(F'(x)=f(x)\) untuk semua \(x\) dalam \(I\).
Kita menggunakan suatu istilah “suatu anti turunan” ketimbang “anti turunan” dalam definisi kita. Kenapa demikian, perhatikanlah contoh berikut.
CONTOH 1:
Carilah suatu anti turunan dari fungsi \(f(x)=4x^3\) pada \((-∞,∞)\).
Penyelesaian:
Kita mencari suatu fungsi \(F\) yang memenuhi \(F'(x)=4x^3\) untuk semua \(x\) riil. Dari pengalaman dengan pendiferensialan kita mengetahui bahwa \(F(x)=x^4\) adalah satu fungsi yang dimaksud.
Akan tetapi, fungsi tersebut bukanlah satu-satunya fungsi untuk penyelesaian contoh ini. Fungsi \(F(x)=x^4+6\) juga memenuhi \(F'(x)=4x^3\); ini juga suatu anti turunan dari \(f(x)=4x^3\). Pada kenyataannya, \(F(x)=x^4+C\), dengan C sebarang konstanta adalah suatu anti turunan dari \(4x^3\) pada \((-∞,∞)\) (lihat Gambar 1)
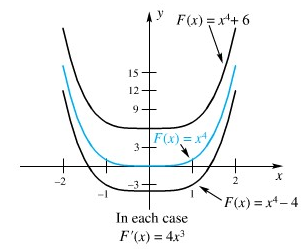
Gambar 1
Sekarang kita dihadapkan pada pertanyaan penting. Apakah setiap anti turunan \(f(x)=4x^3\) berbentuk \(F(x)=x^4+C\) ? Jawabannya adalah ya, karena dua atau lebih fungsi dengan turunan sama yang hanya berbeda dalam konstanta.
Jadi, jika suatu fungsi \(f\) mempunyai suatu anti turunan, ia akan mempunyai keseluruhan famili dan setiap anggota dari famili ini dapat diperoleh dari salah satu di antara mereka dengan jalan menambahkan suatu konstanta yang cocok. Famili fungsi ini kita namakan anti turunan umum dari \(f\).
CONTOH 2:
Carilah anti turunan umum dari \(f(x)=x^2\) pada \((-∞,∞)\).
Penyelesaian:
Anti turunannya adalah \(F(x)=\frac{1}{3} \cdot x^3\) karena memenuhi \( F'(x) = f(x) \) yakni \(F'(x) = \frac{1}{3} \cdot 3x^2 = x^2\). Dengan demikian, anti turunan umumnya adalah \(\frac{1}{3} \cdot x^3+C\).
Notasi Untuk Anti Turunan
Karena kita telah memakai lambang \(D_x\) untuk operasi penentuan suatu turunan, adalah wajar untuk memakai \(A_x\) untuk operasi pencarian anti turunan. Jadi,

Ini adalah notasi yang digunakan oleh beberapa penulis dan sering juga ditemukan dalam beberapa buku terbitan. Akan tetapi, ada notasi yang cukup populer yaitu notasi Leibniz. Maka itu, kita akan lebih sering menggunakan notasi Leibniz tersebut. Ketimbang \(A_x\), Leibniz memakai lambang \(∫… dx\). Ia menuliskan

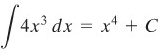
Perhatikan bahwa karena \(∫… dx\) menunjukkan anti turunan terhadap \(x\), dan \(D_x\) menunjukkan turunannya terhadap \(x\), maka \(D_x ∫ f(x) dx = f(x)\).
TEOREMA A: Aturan Pangkat
Jika \(r\) adalah sebarang bilangan rasional, kecuali \(-1\), maka
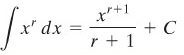
CONTOH 3:
Cari anti turunan yang umum dari \(f(x)=x^{4/3}\).
Penyelesaian:
Dari Teorema A di atas, diperoleh

Perhatikan bahwa untuk anti turunan suatu pangkat dari \(x\) kita perbesar pangkatnya dengan 1 dan membaginya dengan pangkat yang baru.
Dengan mengikuti Leibniz, kita sering kali akan memakai istilah integral tak tentu sebagai ganti anti turunan. Anti penurunan adalah juga mengintegralkan. Dalam lambang \(∫ f(x) \ dx \), \(∫\) disebut tanda integral dan \(f(x)\) disebut integran.
Jadi, kita mengintegralkan integran dan karena itu mendapatkan integral tak tentu. Kemungkinan Leibniz memakai kata sifat 'tak tentu' sebagai pengingat bahwa integral tak tentu selalu mencakup sebarang konstanta.
Integral Tak-Tentu adalah Linear
Anda pasti masih ingat bahwa \(D_x\) adalah suatu operator linear yang mempunyai sifat-sifat berikut

Dengan demikian, kita peroleh teorema sebagai berikut.
TEOREMA B: Integral Tak Tentu adalah sebuah operator linear
Andaikan \(f\) dan \(g\) mempunyai anti turunan (integral tak tentu) dan andaikan \(k\) suatu konstanta. Maka

Bukti:
Untuk memperlihatkan (i) dan (ii), kita cukup mendiferensialkan ruas kanan dan amati bahwa kita memperoleh integran dari ruas kiri.
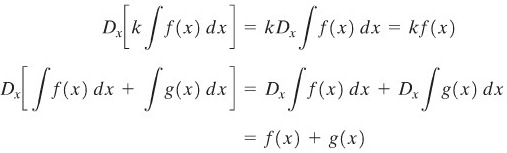
Sifat (iii) menyusul dari (i) dan (ii).
CONTOH 4:
Dengan menggunakan kelinearan \(∫\), hitunglah

Penyelesaian:
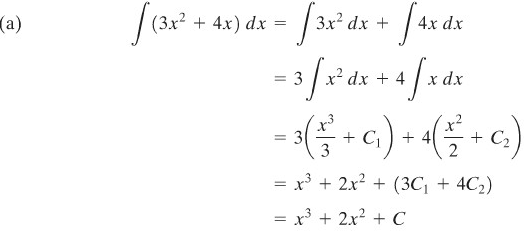
Kemunculan dua konstanta sebarang adalah tidak perlu, karena itu kita dapat gabungkan dalam satu konstanta, yaitu konstanta C.
(b). Perhatikan penggunaan variabel \(u\) sebagai ganti \(x\). Itu baik selama lambang diferensial yang berpadanan adalah \(du\).

Aturan Pangkat yang Diperumum
Ingkat kembali pada Aturan Rantai yang diterapkan pada pangkat suatu fungsi. Jika \(u=g(x)\) adalah suatu fungsi yang dapat didiferensialkan dan \(r\) suatu bilangan rasional \((r≠-1)\), maka

atau, dalam cara penulisan fungsional,

Dari sini kita peroleh suatu aturan penting untuk integral tak tentu.
TEOREMA C: Aturan Pangkat yang Diperumum
Andaikan \(g\) suatu fungsi yang dapat didiferensialkan dan \(r\) suatu bilangan rasional yang bukan \(-1\). Maka

Untuk menerapkan Teorema D, kita harus mampu mengenali fungsi \(g\) dan \(g'\) dalam integran.
CONTOH 5:
Hitunglah

Penyelesaian:
(a) Andaikan \(g(x)=x^4+3x\); maka \(g'(x)=4x^3+3\). Jadi, menurut Teorema D,

(b) Andaikan \(g(x)=\sin{x}\); maka \(g'(x)=\cos{x}\). Jadi,

Sekarang kita dapat melihat mengapa Leibniz menggunakan diferensial \(dx\) dalam cara penulisannya \(∫… dx\). Jika kita tetapkan \(u=g(x)\), maka \(du = g'(x) \ dx\). Karena itu kesimpulan dari Teorema C,

yaitu aturan pangkat yang biasa dengan \(u\) sebagai variabel. Jadi, aturan pangkat yang diperumum hanyalah aturan pangkat yang biasa diterapkan pada fungsi. Tetapi dalam menerapkannya, kita harus selalu yakin bahwa kita mempunyai \(du\) bersama-sama dengan \(u^r\). Contoh-contoh berikut menggambarkan apa yang kita maksudkan.
CONTOH 6:
Hitunglah

Penyelesaian:
(a) Misalkan \(u=x^3+6x\); maka \(du=(3x^2+6) \ dx\). Dengan demikian, \((6x^2+12) \ dx = 2(3x^2+6) \ dx = 2 \ du\), sehingga

(b) Misalkan \(μ=x^2+4\); maka \(du = 2x \ dx\). Dengan demikian,
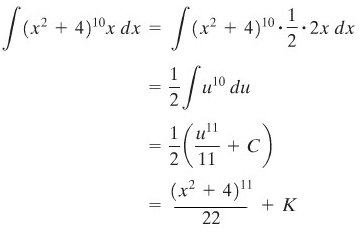
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
The journey of a thousand miles begins with one step.
