www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Limit dan Kekontinuan › Limit Tak Terhingga
Limit Tak Terhingga
Apa yang terjadi pada suatu fungsi g(x) bila x menjadi semakin lama semakin besar? Kita memakai notasi x → ∞ sebagai cara singkat untuk mengatakan bahwa x menjadi semakin besar tanpa batas.
Perhatikan fungsi \(g(x)=\frac{x}{(1+x^2)}\) yang mana grafiknya diperlihatkan dalam Gambar 1. Kita menanyakan pertanyaan ini: Apa yang terjadi pada \(g(x)\) bila \(x\) menjadi semakin lama semakin besar? Dalam lambang, kita menanyakan nilai dari \( \displaystyle{\lim_{x\to ∞}} g(x) \).

Gambar 1
Kita memakai \(x→∞\) sebagai cara singkat untuk mengatakan bahwa \(x\) menjadi semakin besar tanpa batas. Dalam tabel pada Gambar 2, kita telah mendaftarkan nilai-nilai \(g(x)=x/(1+x^2)\) untuk beberapa \(x\). Kelihatan bahwa \(g(x)\) menjadi semakin kecil bilamana \(x\) menjadi semakin besar. Kita tuliskan


Gambar 2.
Untuk \(x→-∞\), kita dapat menuliskan

Dalam mencari nilai limit tak terhingga kita tidak selalu membuat daftar nilai fungsi untuk x menuju tak terhingga seperti diperlihatkan dalam Tabel 2. Melainkan kita dapat gunakan toerema-teorema yang telah kita pelajari terkait limit.
Contoh 1:
Buktikan bahwa
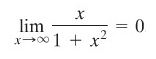
Penyelesaian:
Perhatikan bahwa kita dapat membuktikan limit tersebut dengan membagi pembilang dan penyebut dengan pangkat \(x\) tertinggi yang muncul di penyebut, yakni \(x^2\).

Contoh 2:
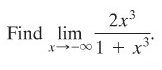
Penyelesaian:
Grafik \(f(x)=\frac{2x^3}{(1+x^3)}\) ditunjukkan pada Gambar 3. Untuk mencari limit ini, bagi pembilang dan penyebut dengan \(x^3\).


Gambar 3
Selanjutnya, pandang grafik \(f(x)=\frac{1}{(x-2)}\), yang diperlihatkan dalam Gambar 4. Ketika x mendekati 2 dari sebelah kiri, fungsi tampak menurun tanpa batas. Begitu pula, ketika \(x\) mendekati 2 dari kanan, fungsi tampak meningkat tanpa batas.
Oleh karena itu, adalah tidak masuk akal untuk menanyakan \( \displaystyle{\lim_{x\to2} \frac{1}{(x-1)} } \) tetapi kita masih dapat menuliskan berikut ini.

Pada limit yang pertama di atas, \(f(x)\) dapat dibuat sebesar yang kita inginkan dengan mengambil \(x\) yang cukup dekat ke 2 dari sebelah kiri. Untuk limit yang kedua, \(f(x)\) dapat dibuat sebesar yang kita inginkan dengan mengambil \(x\) yang cukup dekat ke 2 dari sebelah kanan.
Contoh 3

Penyelesaian:
Grafik \(f(x)=\frac{1}{(x-1)^2}\) diperlihatkan dalam Gambar 4. Ketika \(x→1^+\), penyebut tetap positif tetapi menuju nol, sedangkan pembilang adalah 1 untuk semua \(x\). Jadi, rasio \(1/(x-1)^2\) bisa dibuat besar secara sembarang dengan membatasi \(x\) menjadi dekat 1 di sebelah kanan.
Begitu pula, ketika \(x→1^-\), penyebut adalah positif dan bisa dibuat dekat ke 0 secara sembarang. Karena itu, \(1/(x-1)^2\) bisa dibuat besar secara sembarang dengan membatasi \(x\) dekat ke 1 dari sebelah kiri. Oleh karena itu kita simpulkan bahwa

Karena kedua limit adalah \(∞\), kita dapat juga menuliskan


Gambar 4
Contoh 4

Penyelesaian:
Perhatikan bahwa

Sehingga untuk \(x→2^+\), maka \(x+1→3, \ x-3→-1\), dan \(x-2→0^+\); jadi, pembilang mendekati 3, tetapi penyebut adalah negatif dan mendekati 0. Kita simpulkan

Cukup sekian penjelasan mengenai limit tak terhingga beserta contoh soal dan pembahasannya dalam artikel ini. Semoga bermanfaat.
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Seseorang yang pernah melakukan kesalahan dan tidak pernah memperbaikinya berarti Ia telah melakukan satu kesalahan lagi.
