www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Integral Tak Wajar › Integral dengan Batas Tak Hingga
Integral dengan Batas Tak Hingga
Banyak penerapan integral tentu dalam fisika, ekonomi dan teori peluang yang menghendaki batas atas atau batas bawahnya (atau keduanya) menjadi tak terhingga. Integral demikian dinamakan integral tak wajar dengan batas pengintegralan yang tak terhingga.
Dalam mendefinisikan \(∫_a^b f(x) dx\), sering diandaikan bahwa selang [a,b] terhingga. Walaupun demikian, banyak penerapan integral tentu dalam fisika, ekonomi, dan teori peluang yang menghendaki a atau b (atau keduanya) menjadi tak terhingga. Oleh karena itu, kita akan menjumpai beberapa integral dalam bentuk seperti berikut:

Integral demikian dinamakan integral tak wajar dengan batas pengintegralan yang tak terhingga.
Satu Batas Tak Terhingga
Perhatikan fungsi \(f(x)=xe^{-x}\) dan integral dari \(∫_0^1 xe^{-x} dx\) atau \(∫_0^2 xe^{-x} dx\) atau \(∫_0^b xe^{-x} dx\), di mana b adalah sebarang bilangan positif. Seperti yang bisa anda lihat pada Tabel 1 di bawah, ketika kita meningkatkan batas atas pada integral tentu, nilai integral (area di bawah kurva) akan meningkat.
Tabel 1. Ilustrasi penyelesaian integral \(∫_0^∞ xe^{-x} dx\)

Untuk menyelesaikan \(∫_0^∞ xe^{-x} dx\), kita mulai dengan mengintegralkan dari 0 ke sembarang batas atas, katakanlah \(b\), di mana dengan menggunakan teknik integral parsial memberikan hasil berikut:
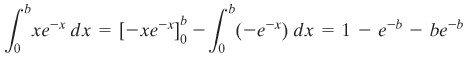
Sekarang, bayangkanlah bahwa nilai \(b\) mendekati takhingga (Lihat Tabel 1 di atas). Seperti yang ditunjukkan pada penghitungan di atas, jika kita membiarkan \(b→∞\), maka nilai integral tentu akan konvergen ke 1. Oleh karena itu, kita dapat mendefinisikan
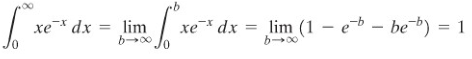
Di bawah ini kita cantumkan definisi yang umum.
DEFINISI:
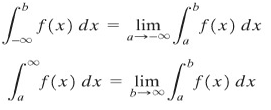
Apabila limit pada ruas kanan ada dan bernilai terhingga, kita katakan bahwa integral tak wajar yang bersangkutan konvergen dan memiliki nilai yang terhingga itu. Jika tidak, integral disebut divergen.
CONTOH 1:
Tentukan, jika mungkin integral \(∫_{-∞}^{-1} xe^{-x^2} \ dx\).
Penyelesaian:

Sehingga,

Kita katakan bahwa integral tak wajar di atas konvergen dengan nilai \(-1/2e\).
CONTOH 2:
Tentukan, jika mungkin, \(∫_0^∞ \sin{x} \ dx\).
Penyelesaian:

Limit terakhir ini tak ada, jadi integral tak wajar di atas adalah divergen. Perhatikan arti geometri integral \(∫_0^∞ \sin{x} \ dx\) itu untuk dapat memahami hasil tersebut (Gambar 1).
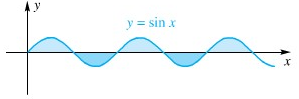
Gambar 1
Kedua batas integral tak terhingga
Kita mulai dengan definisi berikut.
DEFINISI:
Jika baik \(∫_∞^0 f(x) \ dx\) dan \(∫_0^∞ f(x) \ dx\) konvergen, maka \(∫_{-∞}^∞ f(x) \ dx\) dikatakan konvergen dan mempunyai nilai

Jika tidak, \(∫_{-∞}^∞ f(x) \ dx\) dikatakan divergen.
CONTOH 3:
Hitunglah \(∫_{-∞}^∞ \frac{1}{(1+x^2)} \ dx\) atau katakanlah apakah ia konvergen atau divergen.
Penyelesaian:

Karena integran adalah sebuah fungsi genap, maka

Dengan demikian,

CONTOH 4:
Tunjukkan bahwa
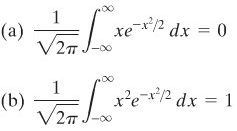
Penyelesaian:
a. Untuk menjawab soal ini, kita perlu mengetahui apa itu fungsi ganjil dan fungsi genap terlebih dahulu. Sekarang perhatikan
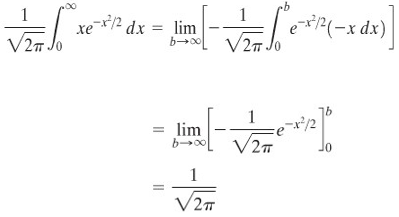
Karena \(xe^{-x^2/2}\) adalah fungsi ganjil, maka

Sehingga,

(b) Karena \(e^{-x^2/2}\) adalah fungsi genap dan karena

maka,
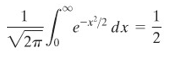
Kita kemudian menerapkan integral parsial dan Aturan I’Hopital.
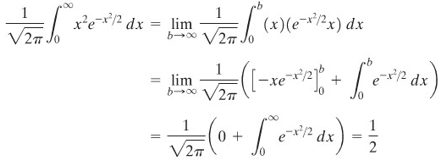
Karena \(x^2 e^{-x^2/2}\) adalah fungsi genap, maka
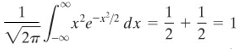
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Kesalahan orang-orang pandai ialah menganggap yang lain bodoh, dan kesalahan orang-orang bodoh ialah menganggap orang lain pandai.
