Kalkulus I   »   Integral   ›  Menghitung Luas Suatu Daerah dengan Integral

Menghitung Luas Suatu Daerah dengan Integral

Dengan menggunakan konsep integral, kita dapat dapat menghitung luas suatu daerah yang yang memiliki batas yang melengkung.

Terdapat dua masalah, keduanya berkenaan dengan geometri, yang memotivasi dua pemikiran terbesar dalam kalkulus. Masalah yang pertama adalah mengenai garis singgung yang membawa kita kepada konsep turunan (derivatif) dan masalah yang kedua adalah mengenai luas yang membawa kita kepada integral tentu. Kita akan fokus pada masalah yang kedua tersebut.

Dalam matematika dasar di bangku sekolah menengah anda harusnya telah diperkenalkan sedikit tentang konsep integral dan bagaimana menghitung luas. Dengan menggunakan rumus baku yang telah diberikan saat itu, anda sekarang harusnya dapat menghitung luas suatu persegi panjang, segitiga, maupun jajaran genjang dengan sangat mudah. Kita tidak akan mengulangnya lagi di sini, tetapi kita akan lebih memfokuskan bagaimana konsep integral ini membawa kita kepada masalah mengenai suatu luas daerah dengan batas yang melengkung.

Bilamana kita meninjau suatu daerah dengan batas melengkung, masalah penentuan luas menjadi lebih sukar. Tetapi lebih dari 2000 tahun yang silam, Archimedes telah menyediakan kunci untuk suatu penyelesaian. Katanya, pandang satu barisan poligon dalam (poligonnya berada dalam suatu lingkaran) yang menghampiri daerah melengkung dengan kecermatan yang semakin besar (Gambar 1).

Sebagai contoh, untuk lingkaran radius 1, pandang poligon dalam beraturan \(P_1,P_2,P_3,…\) dengan 4 sisi, 8 sisi, 16 sisi, limit untuk \(n→∞\) dari luas-luas \(P_n\). Jadi, jika \(A(F)\) menyatakan luas suatu daerah \(F\), maka

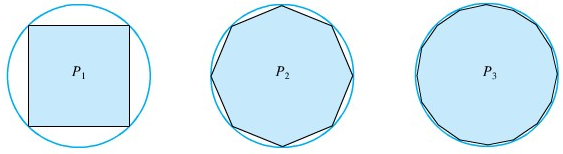
Gambar 1

Archimedes juga melanjutkan bahwa dengan memandang poligon-poligon luar (poligonnya berada di luar suatu lingkaran) \(T_1,T_2,T_3,…\) (Gambar 2), kita akan memperoleh nilai yang sama untuk luas lingkaran radius 1 (yaitu, \(π≈3,14159\)) tidak peduli apakah anda memakai poligon dalam atau poligon luar.

Gambar 2

Sekarang mari kita bahas lebih mendetail apa yang telah dimaksudkan di atas.

Luas Menurut Poligon-Poligon Dalam

Pandang daerah R yang dibatasi oleh parabol \(y=f(x)=x^2\), sumbu-x, dan garis tegak \(x = 2\) (Gambar 3). Kita acu R sebagai daerah di bawah kurva \(y=x^2\) di antara \(x = 0\) dan \(x = 2\). Tujuan kita adalah menghitung luas \(A(R)\).

Gambar 3

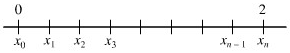
Gambar 4

Partisikan (seperti pada Gambar 4) selang \([0,2]\) menjadi \(n\) selang bagian, masing-masing dengan panjang \(x = 2/n\), memakai titik-titik

Jadi,

Pandang persegi-panjang dengan alas \([x_{1-1}, x_i]\) dan tinggi \(f(x_{i-1}) = x_{i-1}^2\). Luasnya adalah \(f(x_{i-1})Δx\) (lihat bagian kiri dari Gambar 6). Gabungan \(R_n\) dari semua persegi-panjang yang demikian membentuk poligon dalam yang diperlihatkan pada bagian kanan dari Gambar 5.

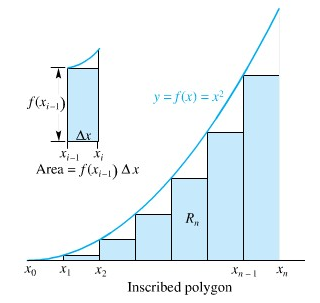
Gambar 5

Luas \(A(R_n)\) dapat dihitung

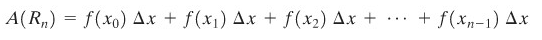
Sekarang,

Jadi,

Kita simpulkan bahwa

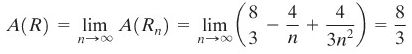
Diagram-diagram pada Gambar 6 akan membantu anda membayangkan apa yang terjadi bilamana \(n\) semakin membesar. Jika \(n\) semakin besar mendekati takhingga maka luas dari seluruh poligon akan sama dengan luas daerah \(R\).

Gambar 6

Luas Menurut Poligon-Poligon Luar

Mungkin anda belum yakin bahwa \(A(R)=8/3\). Kita dapat memberikan lebih banyak fakta. Pandang persegi panjang dengan alas \([x_{i-1}, x_i]\) dan tinggi \(f(x_i)=x_i^2\) (diperlihatkan pada bagian kiri Gambar 7). Luasnya adalah \(f(x_i)Δx\). Gabungan \(S_n\) dari semua persegi panjang yang demikian membentuk suatu poligon luar untuk daerah \(R\), seperti diperlihatkan pada bagian kanan Gambr 7.

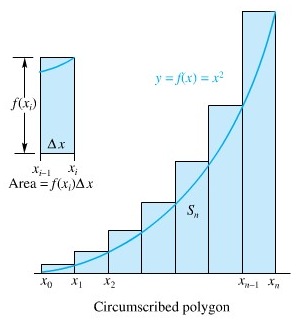
Gambar 7

Luas daerah \(A(S_n)\) dihitung secara analog dengan perhitungan \(A(R_n)\).

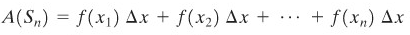
Seperti sebelumnya, \(f(x_i)Δx=x_i^2 Δx = (8/n^3)i^2\), sehingga

Sekali lagi, kita simpulkan bahwa

Jadi, kita telah membuktikan bahwa baik dengan menggunakan poligon dalam maupun poligon luar akan memberikan hasil yang sama untuk luas daerah \(R\).

Sumber:

Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.

Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.