Kalkulus I   »   Fungsi   ›  Fungsi dan Grafik Fungsi

Fungsi dan Grafik Fungsi

Jika variabel \(y\) bergantung pada variabel \(x\) sedemikian rupa sehingga setiap nilai \(x\) menentukan tepat satu nilai \(y\), maka kita mengatakan bahwa \(y\) adalah fungsi dari \(x\).

Salah satu kerangka penting dalam kalkulus adalah analisis hubungan antar variabel. Hubungan semacam itu bisa dideskripsikan dalam bentuk grafik, rumus (formula), secara numerik dengan tabel, atau dalam kata-kata.

Banyak hukum ilmiah dan prinsip-prinsip teknik menggambarkan bagaimana satu kuantitas bergantung pada yang lain. Gagasan ini diresmikan pada tahun 1673 oleh Gottfried Wilhelm Leibniz yang menciptakan istilah fungsi untuk menunjukkan ketergantungan satu kuantitas pada kuantitas lainnya, seperti dijelaskan dalam definisi berikut.

Terdapat 4 metode untuk merepresentasikan fungsi, yaitu

1. Secara numerik dengan tabel
2. Secara aljabar dengan rumus (formula). Misalnya, rumus \(C = 2πr\) menyatakan keliling (\(C\)) dari lingkaran sebagai fungsi jari-jarinya (\(r\)). Hanya ada satu nilai \(C\) untuk setiap nilai \(r\).
3. Secara geometri dengan grafik
4. Secara verbal dengan kata-kata. Sebagai contoh, Hukum Gravitasi Universal Isaac Newton sering dinyatakan sebagai berikut: Gaya tarik gravitasi antara dua benda di Alam Semesta berbanding lurus dengan perkalian massa di antara kedua benda tersebut dan berbanding terbalik dengan kuadrat jarak di antara kedua benda. Atau dapat dinyatakan dalam rumus berikut.

\[ F = G \frac{m_1m_2}{r^2} \]

Grafik Fungsi

Bilamana daerah asal dan daerah hasil sebuah fungsi merupakan bilangan riil, kita dapat membayangkan fungsi itu dengan menggambarkan grafiknya pada suatu bidang koordinat. Dan grafik fungsi \(f\) adalah grafik dari persamaan \(y=f(x)\). Gambar 1 berikut ini menampilkan grafik dari beberapa fungsi.

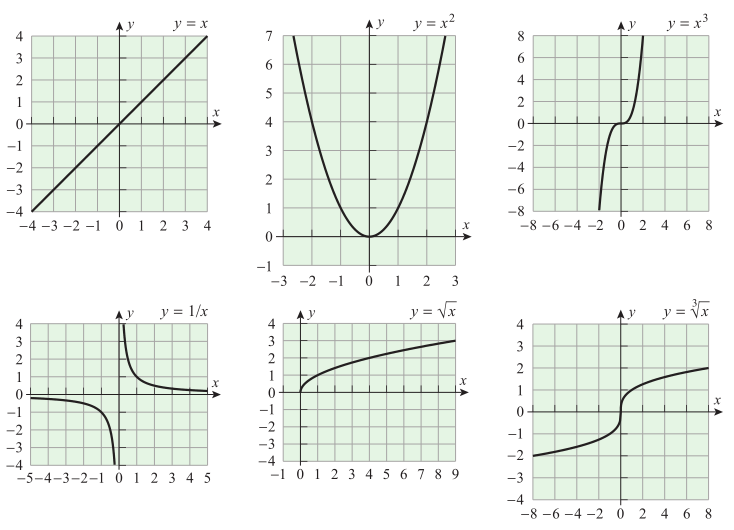
Gambar 1. Contoh grafik dari beberapa fungsi

Grafik dapat memberikan informasi visual yang berharga tentang suatu fungsi. Namun, tidak setiap kurva pada bidang \(xy\) adalah grafik suatu fungsi. Sebagai contoh, perhatikan kurva pada Gambar 2, yang dipotong pada dua titik berbeda, (a, b) dan (a, c), dengan garis vertikal.

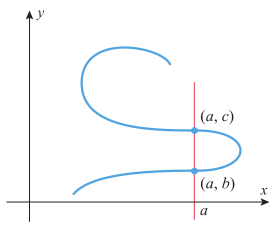
Gambar 2. Kurva ini bukan grafik fungsi

Kurva ini tidak dapat berupa grafik \(y = f(x)\) untuk fungsi \(f\) apa pun. Ini karena

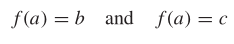
yang mana tidak mungkin, karena \(f\) tidak dapat mempunyai dua nilai yang berbeda untuk \(a\). Kita nyatakan hasil penting ini dalam definisi berikut.

Sebagai contoh, grafik persamaan \( x^2 + y^2 = 25 \) adalah lingkaran berjari-jari 5 yang berpusat pada titik asal (origin) seperti ditampilkan Gambar 3 berikut. Karena garis vertikal memotong grafik lebih dari satu kali, maka persamaan ini tidak mendefinisi \(y\) sebagai fungsi dari \(x\).

Gambar 3. Kurva \( x^2 + y^2 = 25 \)

Sumber:

Anton, Howard., et al. (2012). Calculus, 10th ed. Hoboken: John Wiley & Sons, Inc.

Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.