
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Turunan Fungsi › Turunan Fungsi Implisit - Materi, Contoh Soal dan Pembahasan
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Turunan Fungsi Implisit - Materi, Contoh Soal dan Pembahasan
Secara umum, bentuk fungsi dapat dibedakan menjadi dua yakni fungsi eksplisit dan fungsi implisit. Terdapat dua cara untuk mencari turunan fungsi implisit.
Secara umum, berdasarkan hubungan antara variabel bebas \((x)\) dan tak bebasnya \((y)\), bentuk fungsi dapat dibedakan menjadi dua yakni fungsi eksplisit dan fungsi implisit. Fungsi dengan notasi \(y = f(x)\) disebut fungsi eksplisit yaitu antara peubah bebas dan tak bebasnya dituliskan dalam ruas yang berbeda.
Sebagai contoh, perhatikan beberapa fungsi yang dinyatakan secara eksplisit berikut ini.
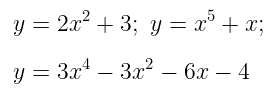
Sementara itu, fungsi implisit yaitu fungsi yang variabel bebas dan variabel tak bebasnya bercampur dalam satu ruas baik di ruas kanan maupun di ruas kiri persamaannya. Perhatikan dua contoh fungsi implisit berikut.
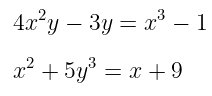
Sejauh ini, pembahasan kita mengenai turunan hanya terbatas pada suatu fungsi eksplisit. Akan tetapi, dalam kenyataannya sering kali kita menjumpai sebuah fungsi implisit dan kita diminta untuk mencari turunan dari fungsi tersebut.
Ada dua cara untuk mencari turunan fungsi implisit. Pertama, lakukan modifikasi pada fungsi implisit sehingga menjadi fungsi eksplisit dan kemudian mencari turunannya seperti pada fungsi eksplisit. Kedua, turunkan kedua ruas persamaan fungsi implisit dan kemudian sederhanakan untuk mendapatkan hasil yang diinginkan. Untuk lebih jelasnya perhatikan beberapa contoh berikut:

Contoh Soal dan Pembahasan
Contoh 1:
Carilah \( \frac{dy}{dx}\) untuk fungsi implisit \(4x^2y - 3y = x^3 - 1\).
Pembahasan:
Cara 1: Modifikasi fungsi implisit sehingga menjadi fungsi eksplisit sebagai berikut.

Kemudian dengan menggunakan rumus turunan pembagian, kita peroleh turunan dari fungsi eksplisit di atas sebagai berikut:

Cara 2: Turunkan kedua ruas persamaannya terhadap \(x\) secara bersamaan, yakni
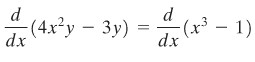
Untuk mencari turunan pada ruas kiri persamaannya, kita bisa memakai aturan perkalian, sedangkan untuk ruas kanannya bisa menggunakan rumus dasar turunan. Kita peroleh berikut ini:
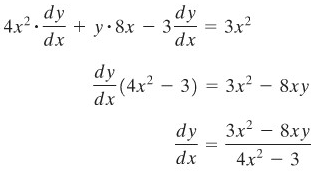
Walaupun jawaban ini kelihatan berlainan dari jawaban yang diperoleh dengan cara pertama, tetapi keduanya adalah sama. Untuk membuktikannya, gantikan \( y = \frac{x^3 - 1}{4x^2 - 3}\) dalam persamaan untuk \(\frac{dy}{dx}\) yang baru saja diperoleh,

Jadi, kesimpulannya adalah baik cara 1 maupun cara 2 menghasilkan jawaban sama. Pertanyaannya adalah menggunakan cara yang mana? Dalam penerapannya, terkadang dengan menggunakan cara 1 saja sudah cukup, tetapi terkadang juga akan dijumpai soal di mana akan jauh lebih mudah menggunakan cara yang kedua.
Contoh 2:
Carilah \(\frac{dy}{dx}\) untuk fungsi implisit \(x^2 + 5y^3 = x + 9\).
Pembahasan:
Kita dapat mencari turunan fungsi implisit ini dengan cara 1 maupun cara 2. Namun, cara 2 tampaknya akan lebih sederhana. Turunkan kedua ruas persamaannya sehingga kita peroleh sebagai berikut.

Baca juga:
Contoh 3:
Carilah turunan dari fungsi implisit berikut: \( 3 \ln xy + \sin y = x^2 \).
Pembahasan:
Fungsi implisit dalam soal ini bisa disederhanakan terlebih dahulu menjadi:

Selanjutnya, dengan menurunkan kedua ruas persamaan fungsi implisit di atas, kita peroleh:
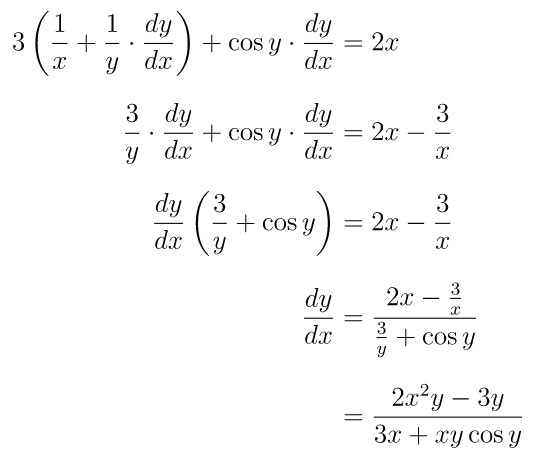
Contoh 4:
Carilah turunan dari fungsi \( y = (\sin x)^x \).
Pembahasan:
Perhatikan bahwa fungsi dalam soal mengandung eksponen yang merupakan variabel sehingga kita tidak bisa menggunakan rumus \( \displaystyle \frac{d}{dx} (x^n) = nx^{n-1} \). Untuk mencari turunan dari fungsi tersebut, kita bisa memberikan logaritma natural pada kedua ruasnya sehingga diperoleh sebuah fungsi implisit.
\begin{aligned} y &= (\sin x)^x \\[8pt] \ln y &= x \ln \sin x \end{aligned}
Untuk mencari turunan dari fungsi implisit di atas, kita bisa turunkan kedua ruas persamaannya, yakni:
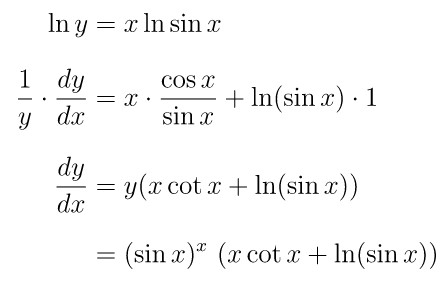
Contoh 5:
Tentukan \( \frac{dy}{dx} \) atau turunan implisit berikut: \( (y+1)^2 = x^2-x \)
Pembahasan:
Diferensialkan kedua ruas pada persamaan implisit terhadap \(x\), yaitu:

Contoh 6:
Tentukan \( \frac{dy}{dx} \) atau turunan implisit berikut: \( x^2+2xy-5y^2 = 1 \)
Pembahasan:
Diferensialkan kedua ruas pada persamaan implisit terhadap \(x\), yaitu:
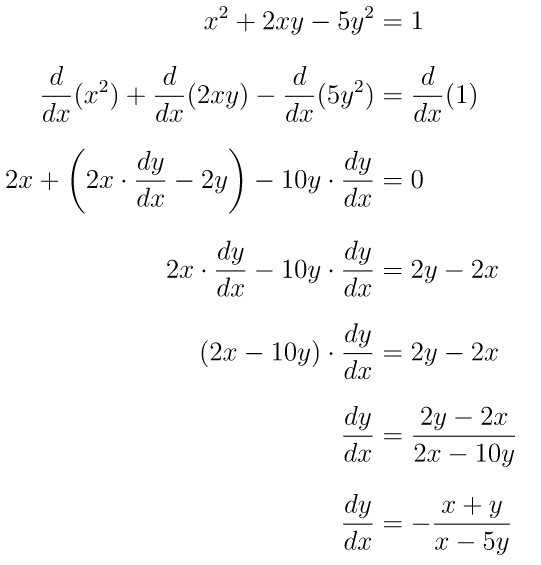

Teorema Turunan Fungsi Implisit
Berbicara mengenai turunan fungsi implisit, ada sebuah teorema penting yang perlu Anda ketahui. Teorema ini akan mempermudah dalam mencari turunan dari sebuah fungsi implisit selain menggunakan dua cara yang telah dijelaskan di atas. Kita nyatakan teorema tersebut berikut ini.
TEOREMA 1:
Jika persamaan \( F(x,y) = 0 \) di mana \( F(x,y) \) adalah fungsi dari \(x\) dan \(y\) yang dapat diturunkan (differentiable), serta \(y\) merupakan fungsi implisit dari \(x\), maka \[ \frac{dy}{dx} = - \frac{F_x(x,y)}{ F_y(x,y) } \]
Jika persamaan \( F(x,y,z)=0 \) di mana \( F(x,y,z) \) adalah fungsi dari \(x, y\) dan \(z\) yang dapat diturunkan (differentiable), serta \(z\) merupakan fungsi implisit dari \(x\) dan \(y\), maka
\begin{aligned} \frac{dz}{dx} &= -\frac{F_x(x,y,z)}{F_z(x,y,z)} \\[8pt] \frac{dz}{dy} &= -\frac{F_y(x,y,z)}{F_z(x,y,z)} \end{aligned}
Sebagai contoh, kita akan menjawab Contoh 1 dan Contoh 2 yang telah kita bahas sebelumnya menggunakan teorema yang dijelaskan di atas.
Contoh 7:
Carilah \( \frac{dy}{dx}\) menggunakan Teorema 1 di atas untuk fungsi implisit \(4x^2y - 3y = x^3 - 1\).
Pembahasan:
Pertama, kita nyatakan fungsi implisitnya ke dalam bentuk \( F(x,y)=0 \), yakni:

Sesuai Teorema 1 di atas, \( \frac{dy}{dx} = - \frac{F_x(x,y)}{ F_y(x,y) } \). Oleh karena itu, kita cari \( F_x(x,y) \) (turunan \(F(x,y)\) terhadap \(x\)) dan \( F_y(x,y) \) (turunan \(F(x,y)\) terhadap \(y\)) terlebih dahulu, yakni:
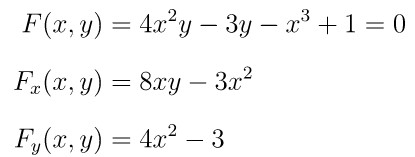
Dengan demikian, kita peroleh \( \frac{dy}{dx}\) yaitu:
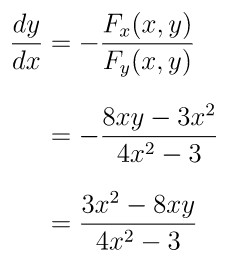
Ingat bahwa fungsi implisit \(4x^2y - 3y = x^3 - 1\) bisa kita tuliskan menjadi \( y = \frac{x^3-1}{4x^2-3} \) dan jika disubstitusikan ke \( \frac{dy}{dx} \) yang kita peroleh di atas, maka

Perhatikan bahwa jawaban yang kita peroleh sama dengan jawaban pada Contoh 1 yang kita bahas sebelumnya.
Contoh 8:
Untuk fungsi implisit \(x^2 + 5y^3 = x + 9\), carilah \(\frac{dy}{dx}\) menggunakan Teorema 1 di atas.
Pembahasan:
Pertama, kita nyatakan fungsi implisitnya ke dalam bentuk \( F(x,y)=0 \), yakni:

Sesuai Teorema 1 di atas, \( \frac{dy}{dx} = - \frac{F_x(x,y)}{ F_y(x,y) } \). Oleh karena itu, kita cari \( F_x(x,y) \) dan \( F_y(x,y) \) terlebih dahulu, yakni:

Dengan demikian, kita peroleh \( \frac{dy}{dx}\) yaitu:

Perhatikan bahwa jawaban yang kita peroleh sama dengan jawaban pada Contoh 2 yang kita bahas sebelumnya.
Dari pembahasan dalam Contoh 7 dan 8 di atas, Anda bisa berkesimpulan bahwa jauh lebih mudah mencari turunan fungsi implisit menggunakan Teorema 1 yang diberikan di atas. Memang benar bahwa lebih mudah dan ringkas mencari turunan implisit menggunakan teorema, tetapi sebaiknya Anda juga paham mencari turunan implisit menggunakan kedua cara yang dijelaskan di awal artikel ini.
Contoh 7 dan 8 di atas merupakan contoh untuk fungsi dua variabel atau peubah. Untuk mencari turunan fungsi implisit dengan tiga variabel, kita bisa lakukan hal yang sama seperti pada fungsi dua variabel. Kita akan membahasnya secara lebih detail pada kesempatan yang lain.
Baca juga:
Cukup sekian penjelasan mengenai turunan fungsi implisit beserta contoh soal dan pembahasannya dalam artikel ini. Semoga bermanfaat.
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Bad things do happen in the world, like war, natural disasters, and disease. But out of those situations always arise stories of ordinary people doing extraordinary things.
