Kalkulus I   »   Turunan Fungsi   ›  Turunan Ordo yang Lebih Tinggi

Turunan Ordo yang Lebih Tinggi

Operasi pendiferensialan mengambil sebuah fungsi \(f\) dan menghasilkan sebuah fungsi baru \(f'\). Jika \(f'\) sekarang kita diferensialkan, kita masih menghasilkan fungsi lain, dinyatakan oleh \(f''\) (dibaca “\(f\) dua aksen”) dan disebut turunan kedua dari \(f\).

Operasi pendiferensialan mengambil sebuah fungsi \(f\) dan menghasilkan sebuah fungsi baru \(f'\). Jika \(f'\) sekarang kita diferensialkan, kita masih menghasilkan fungsi lain, dinyatakan oleh \(f''\) (dibaca “\(f\) dua aksen”) dan disebut turunan kedua dari \(f\). Pada gilirannya ia boleh diturunkan lagi, dengan demikian menghasilkan \(f'''\), yang disebut turunan ketiga, dan seterusnya.

Sebagai contoh, andaikan terdapat fungsi sebagai berikut:

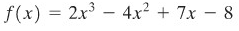
Dengan demikian, diperoleh hasil berikut ini.

Karena turunan dari fungsi nol adalah nol, maka semua turunan tingkat yang lebih tinggi akan nol.

Kita telah memperkenalkan tiga notasi untuk turunan (sekarang disebut juga turunan pertama) dari \(y = f(x)\). Ketiga notasi tersebut adalah

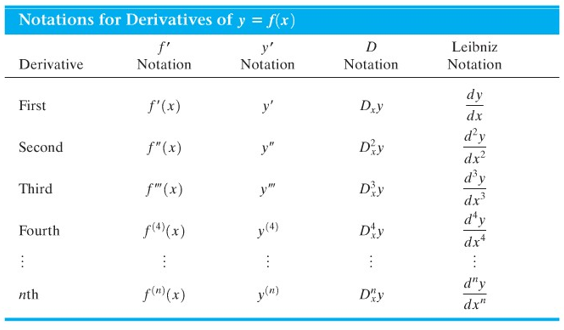
yang mana masing-masing disebut, notasi aksen, notasi d, dan notasi Leibniz. Terdapat sebuah variasi dari cara notasi aksen – yakni, \(y'\) - yang kadang kala akan kita pakai juga. Semua notasi ini mempunyai perluasan untuk turunan tingkat tinggi, seperti diperlihatkan pada Tabel 1.

Tabel 1. Cara penulisan (notasi) untuk turunan dari \(y = f(x)\)

Cukup sekian penjelasan mengenai turunan tingkat tinggi atau turunan untuk ordo yang lebih tinggi beserta contoh soal dan pembahasannya dalam artikel ini. Semoga bermanfaat.

Sumber:

Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.

Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.