www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Aplikasi Integral › Luas Daerah di Atas dan di Bawah Sumbu-x
Luas Daerah di Atas dan di Bawah Sumbu-x
Salah satu penerapan penting integral ialah untuk menghitung luas daerah yang berada di atas atau di bawah sumbu \(x\).
Pembahasan singkat mengenai cara menghitung luas suatu daerah pada artikel sebelumnya memberikan dasar tentang definisi integral tentu. Setelah konsep tersebut benar-benar dipahami, kita akan menggunakan integral tentu untuk menghitung luas daerah-daerah yang bentuknya rumit.
Pertama, kita akan memulai dengan menghitung daerah yang berada di atas sumbu x, kemudian daerah di bawah sumbu x, dan terakhir luas daerah yang berada di antara dua kurva.
Daerah di atas sumbu x.
Andaikan \(y=f(x)\) menentukan persamaan sebuah kurva pada bidang \(xy\) dan andaikan \(f\) kontinu dan tak-negatif pada interval \(a < x < b\) (Perhatikan Gambar 1). Perhatikan daerah \(R\) yang dibatasi oleh grafik-grafik dari \(y = f(x), x = a, x = b\), dan \(y = 0\). Kita menyatakan \(R\) sebagai daerah di bawah \(y = f(x)\) antara \(x = a\) dan \(x = b\). Luas daerah tersebut yaitu \(A(R)\), ditentukan oleh rumus berikut ini.


Gambar 1
CONTOH 1:
Tentukan luas daerah \(R\) di bawah kurva \(y=x^4-2x^3+2\) antara \(x=-1\) dan \(x=2\).
Pembahasan:
Daerah \(R\) diperlihatkan pada Gambar 2.

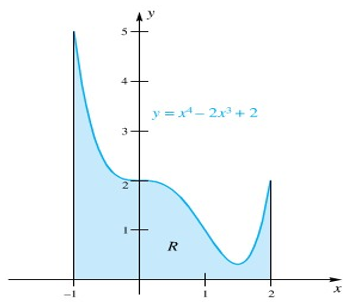
Gambar 2.
Daerah di bawah sumbu x.
Luas daerah dinyatakan oleh bilangan yang tak negatif. Apabila grafik \(y=f(x)\) terletak di bawah sumbu-x maka \(∫_a^b f(x) \ dx\) adalah bilangan yang negatif, sehingga tak dapat menggambarkan suatu luas. Oleh karena itu, kita perlu mengalikan bilangan itu dengan negatif untuk luas daerah yang berada di bawah sumbu x
CONTOH 2:
Tentukan luas daerah \(R\) yang dibatasi oleh \(y=\frac{x^2}{3}-4\), sumbu \(z\), \(x = -2\) dan \(x = 3\).
Pembahasan:
Daerah \(R\) diperlihatkan pada Gambar 3.
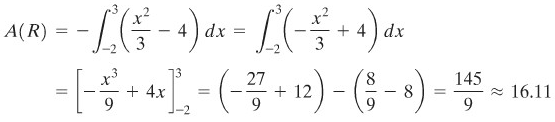

Gambar 3.
CONTOH 3:
Tentukan luas daerah \(R\) yang dibatasi oleh \(y=x^3-3x^2-x+3\), ruas sumbu \(x\) antara \(x = -1\) dan \(x = 2\), dan oleh garis \(x = 2\).
Pembahasan:
Daerah \(R\) adalah daerah yang diarsir pada Gambar 4. Perhatikan bahwa ada sebagian di atas sumbu \(x\) \( (R_1) \) dan ada yang di bawah sumbu \(x\) \( (R_2) \). Luas masing-masing bagian ini harus dihitung secara terpisah. Daerah \(R\) yang diperlihatkan pada Gambar 4 memotong sumbu \(x\) di -1, 1, dan 3 sehingga
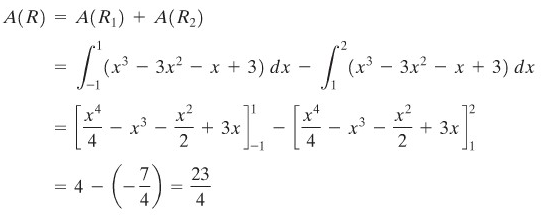

Gambar 4.
Demikian penjelasan mengenai penerapan integral untuk menghitung luas daerah yang berada di atas maupun di bawah sumbu x. Untuk menghitung luas daerah yang berada di antara dua kurva akan dibahas pada artikel selanjutnya. Klik link berikut ini: Penerapan Integral untuk Menghitung Luas Daerah Antara Dua Kurva
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Saya memiliki filosofi yang sederhana: isi apa yang kosong, kosongkan apa yang terlalu penuh.
