www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Integral Tak Wajar › Integral dengan Fungsi Integran Tak Wajar
Integral dengan Fungsi Integran Tak Wajar
Agar suatu fungsi dapat diintegralkan dalam arti yang biasa, fungsi tersebut haruslah terbatas. Namun, dalam kondisi tertentu akan dijumpai integral dengan fungsi yang tak terbatas. Integral yang demikian disebut integral yang tak wajar dengan integran yang tak terbatas.
Berikut ini diberikan salah satu contoh integral yang kelihatannya cukup sederhana, tetapi tidaklah benar demikian.
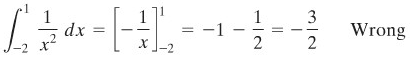
Apabila kita perhatikan grafik pada Gambar 1 tampak ada sesuatu yang aneh. Sebab jawaban integral (jika memang ada) tentunya harus suatu bilangan yang positif. Mengapa? Karena daerah kurva ada di atas sumbu-x. Lantas, di manakah letak kesalahan dalam perhitungan integral tersebut?
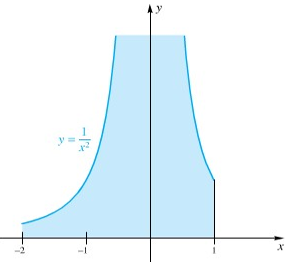
Gambar 1
Seperti diketahui, agar suatu fungsi dapat diintegralkan dalam arti yang biasa, fungsi tersebut haruslah terbatas. Dalam contoh di atas, fungsi \(f(x)=1/x^2\) merupakan fungsi yang tak terbatas. Jadi tak dapat diintegralkan dalam arti yang biasa. Kita katakan bahwa \(∫_{-2}^1 x^{-2} \ dx\) adalah integral yang tak wajar dengan integran tak terhingga atau integran yang tak terbatas.
Pada artikel ini kita akan mendefinisikan dan membahas integral-integral itu. Pertama, kita akan membahas integral dengan integral tak terhingga pada titik ujung suatu selang. Kemudian dilanjutkan dengan integral dengan integran tak terhingga pada sebuah titik dalam.
Integran yang Tak Terhingga pada Titik Ujung Suatu Selang.
Kita berikan definisi integral yang integrannya menuju tak terhingga di titik ujung sebelah kanan selang pengintegralan. Kita juga akan dapatkan definisi hampir serupa untuk integran yang menuju tak terhingga di titik ujung sebelah kiri.
DEFINISI:
Andaikan \(f\) kontinu pada selang setengah-buka \([a,b)\) dan misalkan bahwa
\[ \displaystyle{\lim_{x\to b^{-1}} |f(x)| = \infty} \]
Maka

asalkan limit itu ada dan terhingga. Dalam hal ini dikatakan bahwa integral tersebut konvergen. Dalam hal yang lain, integral disebut divergen.
CONTOH 1:
Jika mungkin hitunglah integral tak-wajar
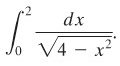
Penyelesaian:
Integran menuju tak terhingga apabila \(x\) menuju 2, sehingga tidak bisa diselesaikan dengan integral dalam arti yang biasa. Dalam hal ini, kita kerjakan sesuai dengan yang telah dijelaskan di atas.

CONTOH 2:
Jika mungkin hitunglah integral tak-wajar
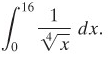
Penyelesaian:
Integran menuju tak terhingga apabila \(x\) menuju 0, sehingga tidak bisa diselesaikan dengan integral dalam arti yang biasa. .
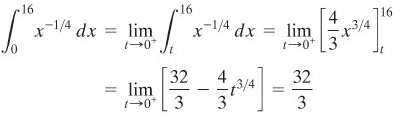
CONTOH 3:
Jika mungkin hitunglah integral tak-wajar
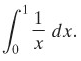
Penyelesaian:
Integran menuju tak terhingga apabila \(x\) menuju 0. Dengan demikian,

Jadi, integral ini divergen.
CONTOH 4:
Buktikan bahwa \(∫_0^1 1/x^p \ dx\) konvergen untuk \(p < 1\) tetapi divergen bila \(p ≥ 1\).
Penyelesaian:
Dalam contoh 3 telah dibahas kasus untuk \(p = 1\). Apabila \(p≠1\) kita peroleh.

Integran yang Tak Terhingga pada Sebuah Titik Dalam
Integral \(∫_{-2}^1 1/x^2 \ dx\) adalah sebuah contoh untuk integran yang tak-terhingga pada sebuah titik dalam (ada nilai di antara -2 dan 1 yang membuat fungsi tersebut tak-terhingga). Perhatikan bahwa integran ini tak terhingga pada \(x = 0\). Definisi tepatnya adalah sebagai berikut:
DEFINISI:
Andaikan \(f\) merupakan fungsi yang kontinu pada \([a,b]\) kecuali di sebuah bilangan \(c\), di mana \(a < c < b\), dan anggaplah
\[ \displaystyle{\lim_{x\to c} |f(x)| = \infty} \]
Maka kita mendefinisikan

asalkan kedua integral pada ruas kanan konvergen. Jika tidak, kita katakan bahwa \(∫_a^b f(x) dx\) divergen.
CONTOH 5:
Buktikan bahwa \(∫_{-2}^1 1/x^2 \ dx\) divergen.
Penyelesaian:

Menurut Contoh 4, integral kedua pada ruas kanan divergen. Jadi integral yang diberikan adalah divergen.
CONTOH 6:
Jika mungkin, hitunglah integral tak-wajar

Penyelesaian:
Integran kita menuju tak terhingga di \(x = 1\) (Gambar 2). Jadi,
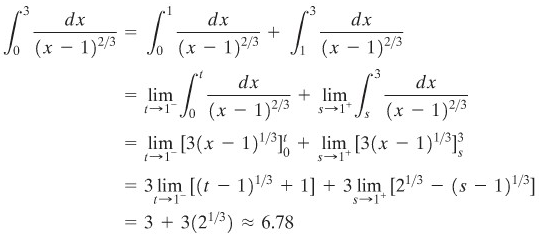
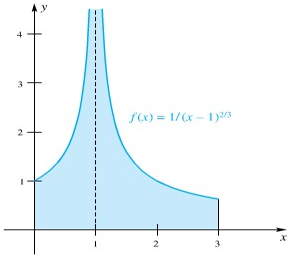
Gambar 2.
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Dia yang mampu menguasai orang lain memang kuat. Tapi dia yang mampu menguasai dirinya sendiri, itulah yang lebih dahsyat.
