Kalkulus I   »   Fungsi   ›  Fungsi Eksponensial dan Eksponensial Natural

Fungsi Eksponensial dan Eksponensial Natural

Di antara semua kemungkinan basis untuk fungsi eksponensial, terdapat satu basis khusus yang memainkan peran penting dalam kalkulus. Basis itu, dinyatakan dengan huruf e. Fungsi eksponensial dengan basis e dinamakan fungsi ekponensial natural.

Dari pelajaran terkait aljabar kita tahu bahwa jika b adalah bilangan riil taknol, maka pangkat bilangan taknol dari b didefinisikan oleh

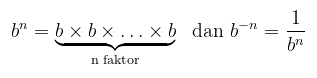
Dan jika \(n = 0\), maka \(b^0=1\). Selain itu, jika \(p/q\) adalah bilangan rasional positif, maka

Jika \(b\) adalah negatif, maka beberapa pangkat pecahan dari \(b\) akan mempunyai nilai imaginer – misalnya, \((-2)^{1/2}=\sqrt{-2}\). Untuk menghindari kesulitan ini, kita akan mengasumsikan bahwa \(b > 0\), bahkan jika kita tidak menyatakannya secara eksplisit.

Keluarga fungsi eksponen

Sebuah fungsi bentuk \(f(x)=b^x\), di mana \(b>0\), disebut fungsi eksponensial dengan basis \(b\). Beberapa contoh fungsi eksponensial diberikan berikut ini

Perhatikan bahwa fungsi eksponensial mempunyai basis konstanta dan variabel eksponen. Dengan demikian, fungsi seperti \(f(x)=x^2\) dan \(f(x)=x^π\) tidak akan diklasifikasikan sebagai fungsi eksponensial, karena fungsi-fungsi tersebut mempunyai sebuah basis variabel dan eksponen konstanta.

Gambar 1 mengilustrasikan bahwa grafik \(y=b^x\) mempunyai tiga bentuk umum yang tergantung pada nilai \(b\), yakni ketika (i) (0 < b < 1), (ii) \(b > 1\), dan (iii) \(b=1\).

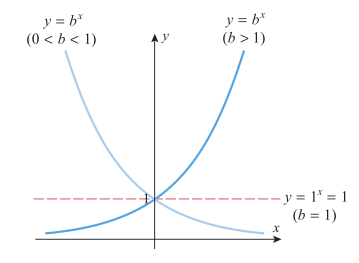
Gambar 1.

Grafik \(y=b^x\) di atas mempunyai sifat-sifat berikut:

1. Grafik melalui titik (0,1) karena \(b^0=1\).
2. Jika \(b > 1\), nilai \(b^x\) meningkat ketika \(x\) meningkat. Jika anda menelusuri grafik dari kiri ke kanan, nilai \(b^x\) meningkat secara tak terbatas. Jika anda menelusuri grafik dari kanan ke kiri, nilai \(b^x\) menurun menuju nol tetapi tidak pernah mencapai nol. Oleh karena itu, sumbu-\(x\) merupakan sebuah asimtot horisontal dari grafik \(b^x\).
3. Jika \(0 < b < 1\), nilai \(b^x\) menurun ketika \(x\) meningkat. Jika anda menelusuri grafik \(y=b^x\) dari kiri ke kanan, nilai \(b^x\) menurun menuju nol tetapi tidak pernah mencapai nilai nol. Karena itu, sumbu \(x\) merupakan asimtot horisontal dari grafik \(b^x\). Jika anda menelusuri grafik dari kanan ke kiri, nilai \(b^x\) meningkat secara tak terbatas.
4. Jika \(b = 1\), maka nilai \(b^x\) adalah konstan.

Beberapa anggota khusus dari keluarga fungsi eksponensial digrafikkan pada Gambar 2 berikut.

Gambar 2.

Gambar 2 di atas mengilusrasikan bahwa grafik \(y=(1/b)^x\) merupakan pencerminan dari grafik \(y=b^x\) terhadap sumbu-\(y\). Ini karena dengan menggantikan \(x\) dengan \(–x\) dalam persamaan \(y=b^x\) menghasilkan

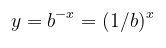
Fungsi ini juga menyampaikan bahwa untuk \(b > 1\), semakin besar basis \(b\), semakin cepat fungsi \(f(x)=b^x\) meningkat untuk \(x > 0\).

Daerah asal dan daerah hasil dari fungsi eksponensial \(f(x)=b^x\) juga bisa ditemukan dengan mengkaji Gambar 1.

1. Jika \(b > 0\), maka \(f(x)=b^x\) terdefinisi dan mempunyai nilai riil untuk setiap nilai riil \(x\), sehingga daerah asal natural untuk setiap fungsi eksponensial adalah \((-∞,+∞)\).
2. Jika \(b > 0\) dan \(b≠1\), maka seperti yang dinyatakan sebelumnya, grafik \(y=b^x\) meningkat secara tak terbatas ketika grafik ditelusuri dalam satu arah dan menurun menuju nol tetapi tidak pernah mencapai nol ketika ditelusuri dalam arah yang lain. Ini mengimplikasikan bahwa daerah hasil dari \(f(x)=b^x\) adalah \((0,+∞)\).

Sifat-sifat \(a^x\)

Teorema kita yang pertama memperlihatkan sifat-sifat tentang eksponen yang lazimnya berlaku.

Fungsi Eksponensial Natural

Di antara semua kemungkinan basis untuk fungsi eksponensial, terdapat satu basis khusus yang memainkan peran penting dalam kalkulus. Basis itu, dinyatakan dengan huruf \(e\), merupakan bilangan tak rasional di mana nilainya sampai enam angka di belakang koma adalah

Basis ini penting dalam kalkulus karena, seperti akan kita buktikan nanti, bahwa \(b = e\) merupakan satu-satunya basis di mana kemiringan garis singgung untuk kurva \(y=b^x\) pada sebarang titik P pada kurva sama dengan koordinat \(y\) pada \(P\). Dengan demikian, misalnya, garis singgung untuk \(y=e^x\) pada (0,1) mempunyai kemiringan 1. (Gambar 4).

Gambar 4.

Fungsi \(f(x)=e^x\) dinamakan fungsi eksponensial natural. Untuk menyederhanakan penulisan, fungsi eksponensial natural kadang dituliskan sebagai \(\exp⁡(x)\), di mana kasus hubungan \(e^{x_1+x_2}=e^{x_1} \cdot e^{x_2}\) akan dinyatakan sebagai

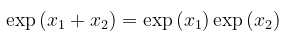
Konstanta \(e\) juga muncul dalam konteks grafik persamaan

Seperti ditunjukkan pada Gambar 5, \(y = e\) merupakan asimptot horisontal dari grafik ini. Akibatnya, nilai \(e\) bisa diaproksimasi untuk sebarang tingkat keakuratan dengan menghitung persamaan 3 untuk \(x\) sampai cukup besar dalam nilai mutlak (Tabel 1).

Gambar 5.

Tabel 1.

Sumber:

Anton, Howard., et al. (2012). Calculus, 10th ed. Hoboken: John Wiley & Sons, Inc.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.