www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Teknik Pengintegralan › Aturan Tanzalin dalam Integral Parsial
Aturan Tanzalin dalam Integral Parsial
Dalam teknik integral parsial, terdapat aturan penting yang dikenal Aturan Tanzalin. Aturan ini dapat memudahkan kita untuk mencari integral berdasarkan teknik integral parsial.
Sebagaimana telah kita pelajari bahwa salah satu cara untuk menyelesaikan integral dikenal dengan teknik integral parsial. Teknik ini biasanya dipakai ketika teknik integral dengan substitusi tidak dapat diterapkan untuk menyelesaikan integral tersebut. Integral parsial digunakan untuk mencari integral dari perkalian dua buah fungsi.
Rumus integral parsial, yaitu:
\[ \int u \ dv = uv - \int v \ du \]
Jika integralnya ada batas atau disebut integral tertentu, maka rumus integral parsialnya menjadi
\[ \int_a^b u \ dv = [uv]_a^b - \int_a^b v \ du \]
Dalam teknik integral parsial, terdapat sebuah aturan penting yang dikenal dengan Aturan Tanzalin. Aturan ini dapat memudahkan kita untuk mencari integral berdasarkan teknik integral parsial.
Dalam Aturan Tanzalin, kita akan membentuk sebuah tabel yang terdiri dari 4 kolom di mana kolom pertama berisi fungsi yang akan kita turunkan, kolom kedua berisi fungsi yang akan diintegralkan, kolom ketiga berisi tanda positif dan negatif, dan kolom keempat berisi hasil perkalian silang dari kolom pertama dan kedua dengan tanda yang sesuai.
Sebagai contoh, untuk mencari \(\int f(x) \cdot g(x) \ dx\) menggunakan Aturan atau Teknik Tanzalin, kita membuat tabel sebagai berikut:

Pada kolom pertama yakni Kolom Turunan, kita tempatkan fungsi polinomial yang paling sederhana di antara \(f(x)\) dan \(g(x)\) (di sini kita misalkan \(f(x)\) sebagai yang paling sederhana) yang mana ketika diturunkan hingga ke sekian kalinya hasilnya akan bernilai nol. Pada tabel ini dimisalkan bahwa turunan ke-n nya bernilai nol, yakni \(f^{(n)} (x)=0\).
Selanjutnya, pada kolom kedua yakni Kolom Integral, kita tempatkan fungsi lainnya \((g(x))\) lalu diintegralkan sebanyak \(n\) kali.
Pada kolom ketiga yakni Kolom Tanda, kita berikan tanda + dan – secara bergantian. Terakhir, pada kolom keempat, yakni Kolom Perkalian Warna Sama, kita kalikan besaran-besaran dengan warna yang sama seperti tampak pada tabel di atas. Perhatikan bahwa hasil perkalian baris yang berwarna biru dan hijau tidak mengubah tanda karena pada kolom ketiga tandanya +.
Sementara itu, hasil perkalian baris yang berwarna kuning berubah tanda menjadi negatif (dikalikan negatif), karena pada kolom ketiga tandanya bernilai "-". Begitu seterusnya untuk perkalian baris selanjutnya berganti tanda hingga pada baris di mana \(f^{(n)} (x)=0\).
Hasil dari integral adalah penjumlahan setiap baris pada Kolom Perkalian Warna Sama ditambahkan dengan sebuah konstanta real.
Untuk lebih jelasnya, perhatikan beberapa contoh soal berikut:
Contoh Soal Aturan Tanzalin
Berikut ini adalah kumpulan contoh soal integral yang penyelesaiannya menggunakan teknik integral parsial dengan Aturan Tanzalin.
CONTOH 1:
Selesaikan \( \displaystyle \int 5x \ (1-x)^6 \ dx \) menggunakan Aturan Tanzalin.
Pembahasan:
Perhatikan bahwa polinomial paling sederhana antara \(5x\) dan \((1-x)^6\) adalah \(5x\) sehingga kita menaruhnya pada Kolom Turunan dan \((1-x)^6\) pada Kolom Integral. Berikut hasil yang kita peroleh:
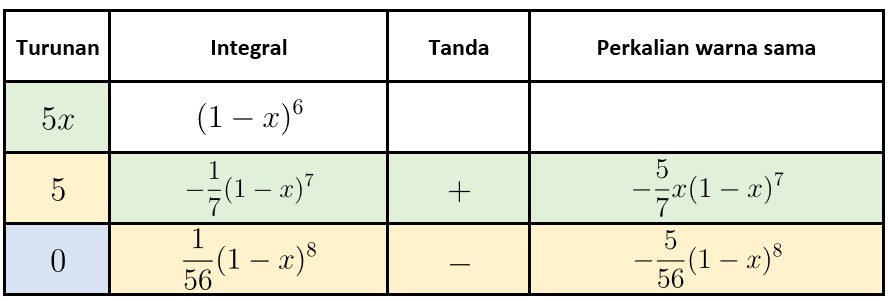
Dengan demikian, kita peroleh:
\begin{aligned} \int 5x \ (1-x)^6 \ dx = -\frac{5}{7}x (1-x)^7 - \frac{5}{56}(1-x)^8 + C \end{aligned}
CONTOH 2:
Selesaikan \( \displaystyle \int x^2 \ \cos x \ dx \) menggunakan Aturan Tanzalin.
Pembahasan:
Perhatikan bahwa kita menempatkan \(x^2\) pada Kolom Turunan karena jika diturunkan hingga kesekian kalinya hasilnya bernilai nol, dan \( \cos x \) pada Kolom Integral. Berikut hasil yang kita peroleh:

Dengan demikian, kita peroleh:
\begin{aligned} \int x^2 \cos x \ dx &= x^2 \sin x + 2x \cos x - 2 \sin x + C \\[5pt] &= (x^2-2) \sin x + 2x \cos x + C \end{aligned}
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Be a prisoner of the past or a pioneer of the future. The choice is yours.
