www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Fungsi Gamma dan Fungsi Beta › Penyelesaian Integral Trigonometri dengan Fungsi Beta
Penyelesaian Integral Trigonometri dengan Fungsi Beta
Dalam beberapa kasus, kita akan menjumpai bentuk pengintegralan yang melibatkan fungsi trigonometri. Ada beberapa bentuk integral trigonometri yang dapat diselesaikan dengan mudah menggunakan fungsi beta.
Dalam beberapa kasus, kita mungkin akan menjumpai bentuk pengintegralan yang melibatkan fungsi trigonometri. Di beberapa artikel sebelumnya, kita telah mencoba menyelesaikan integral tersebut dengan menggunakan teknik integral pangkat trigonometri dan teknik substitusi trigonometri.
Namun, ada kalanya kita tidak bisa menyelesaikan integral tersebut dengan cara demikian atau bisa diselesaikan tapi membutuhkan proses yang cukup rumit.
Di sini kita akan melihat bahwa ada beberapa bentuk integral trigonometri yang dapat diselesaikan dengan mudah menggunakan fungsi beta. Perhatikanlah dua contoh khusus integral trigonometri berikut

Dua integral ini tampak rumit, tapi sebenarnya sangat mudah diselesaikan dengan menggunakan bantuan fungsi beta. Untuk itu, mari kita lihat bagaimana fungsi beta membantu kita menyelesaikan integral tersebut.
Sebagaimana telah kita ketahui bahwa fungsi beta dinyatakan sebagai
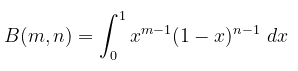
Selain itu, fungsi Beta juga dapat dinyatakan dalam bentuk integral trigonometri yaitu:
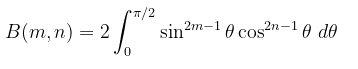
Rumus fungsi beta dalam bentuk trigonometri di atas dapat dibuktikan dengan sangat mudah. Perhatikanlah bahwa ketika \( x = \sin^2 θ \) disubstitusikan ke dalam persamaan fungsi beta, kita peroleh

Ingat bahwa turunan dari \( x = \sin^2 θ \) adalah \(dx/dθ = 2 \sin θ \ \cos θ\), sehingga \( dx = 2 \sin θ \ \cos θ \ dθ \).
Sekarang kita siap untuk menjawab dua contoh integral trigonometri yang diberikan di atas.
Contoh 1:
Selesaikanlah integral berikut:
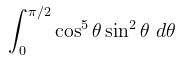
Pembahasan:
Ingat kembali rumus

Integral pada Contoh 1 ini mirip dengan rumus fungsi Beta dalam integral trigonometri, sehingga

Dengan demikian,

Contoh 2:
Selesaikanlah integral berikut:

Pembahasan:
Anda mungkin masih ingat bahwa

Dengan demikian,

Berdasarkan rumus fungsi Beta dalam bentuk integral trigonometri, maka diperoleh

Dengan demikian, kita peroleh

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Hidup adalah mimpi bagi mereka yang bijaksana, permainan bagi mereka yang bodoh, komedi bagi mereka yang kaya, dan tragedi bagi mereka yang miskin.
