www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Aplikasi Turunan › Aplikasi Turunan: Menentukan Nilai Maksimum dan Minimum Fungsi
Aplikasi Turunan: Menentukan Nilai Maksimum dan Minimum Fungsi
Dalam hidup ini, kita sering menghadapi masalah guna mendapatkan jalan terbaik untuk melakukan sesuatu. Kadang kala masalah tersebut dapat dirumuskan sehingga akan melibatkan memaksimumkan dan meminimumkan fungsi tertentu.
Dalam hidup ini, kita sering menghadapi masalah guna mendapatkan jalan terbaik untuk melakukan sesuatu. Sebagai contoh, seorang petani ingin memilih kombinasi hasil panen yang dapat menghasilkan keuntungan terbesar. Seorang dokter akan menentukan dosis obat yang terkecil untuk menyembuhkan suatu penyakit. Seorang kepala pabrik akan menekan sekecil mungkin biaya pendistribusian produknya.
Kadang kala masalah tersebut dapat dirumuskan sehingga akan melibatkan memaksimumkan dan meminimumkan fungsi tertentu. Bila demikian, metode kalkulus menyediakan sarana yang ampuh untuk memecahkan masalah seperti itu.
Andaikan kita mengetahui fungsi \(f\) dan domain (daerah asal) \(S\) seperti pada Gambar 1. Tugas kita yang pertama adalah menentukan apakah \(f\) memiliki nilai maksimum dan nilai minimum pada \(S\). Anggap bahwa nilai-nilai tersebut ada, kita ingin mengetahui lebih lanjut di mana dalam \(S\) nilai-nilai itu berada.

Gambar 1
Kita mulai dengan memperkenalkan suatu definisi yang tepat.
DEFINISI:
Andaikan \(S\), daerah asal \(f\), memuat titik \(c\). Kita katakan bahwa
- \(f(c)\) adalah nilai maksimum \(f\) pada \(S\) jika \(f(c)≥f(x)\) untuk semua \(x\) dalam \(S\);
- \(f(c)\) adalah nilai minimum \(f\) pada \(S\) jika \(f(c)≤f(x)\) untuk semua \(x\) dalam \(S\);
- \(f(c)\) adalah nilai ekstrim \(f\) pada \(S\) jika ia adalah nilai maksimum atau nilai minimum.
- fungsi yang ingin kita maksimalkan atau minimalkan adalah fungsi tujuan (objective function).
Pertanyaan Eksistensi.
Apakah \(f\) mempunyai nilai maksimum (atau minimum) pada \(S\)? Jawabannya tergantung pertama-tama pada himpunan \(S\) tersebut. Ambillah \(f(x)=1/x\) pada \(S=(0,∞)\); fungsi ini tidak mempunyai nilai maksimum ataupun minimum (Gambar 2). Akan tetapi, fungsi yang sama pada \(S = [1,3]\) mempunyai nilai maksimum \(f(1)=1\) dan nilai minimum \(f(3)=1/3\). Pada \(S = (1,3]\), \(f\) tidak mempunyai nilai maksimum sedangkan nilai minimumnya adalah \(f(3)=1/3\).

Gambar 2
Jawaban apakah \(f\) mempunyai nilai maksimum atau minimum juga tergantung pada tipe fungsi. Ambillah contoh fungsi tak kontinu \(g\) (Gambar 3) yang didefinisikan oleh

Pada \(S=[1,3], \ g\) tidak mempunyai nilai maksimum (menjadi cukup dekat ke 2 tetapi tidak pernah mencapainya). Tetapi \(g\) mempunyai nilai minimum \(g(2)=0\).

Gambar 3
Terdapat sebuah teorema bagus yang menjawab pertanyaan eksistensi untuk beberapa masalah yang muncul dalam praktek.
TEOREMA A: Teorema Eksistensi Max-Min
Jika \(f\) kontinu pada interval tertutup \([a,b]\), maka \(f\) mencapai nilai maksimum dan nilai minimum.
Perhatikan kata-kata kunci: ‘\(f\) harus kontinu dan himpunan \(S\) harus berupa selang tertutup’.
Di mana terjadinya nilai-nilai ekstrim?
Biasanya fungsi yang ingin kita maksimumkan atau minimumkan akan mempunyai suatu selang \(I\) sebagai daerah asalnya. Tetapi selang ini boleh berupa sebarang dari sembilan tipe selang yang telah dibahas. Beberapa dari selang ini memuat titik-titik ujung; beberapa tidak.
Misalnya, \(I=[a,b]\) memuat titik ujung dua-duanya; [a,b) hanya memuat titik ujung kiri; \((a,b)\) tidak memuat titik ujung manapun. Nilai-nilai ekstrim sebuah fungsi yang didefinisikan pada selang tertutup sering kali terjadi pada ttik-titik ujung (lihat Gambar 4).

Gambar 4
Jika \(c\) sebuah titik di mana \(f'(c)=0\), kita sebut \(c\) titik stasioner. Nama itu diturunkan dari fakta bahwa pada titik stasioner, grafik \(f\) mendatar, karena garis singgung mendatar. Nilai-nilai ekstrim juga sering kali terjadi pada titik-titik stasioner (lihat Gambar 5).
Akhirnya , jika \(c\) adalah titik dalam dari \(I\) di mana \(f'\) tidak ada, kita sebut \(c\) titik singular. Ini merupakan titik di mana grafik \(f\) mempunyai sudut tajam, garis singgung vertikal atau mungkin berupa lompatan (atau di dekatnya ia bergoyang sangat buruk). Nilai-nilai ekstrim dapat terjadi pada titik-titik singular (Gambar 6), walaupun dalam masalah-masalah praktis hal ini sangat jarang terjadi.
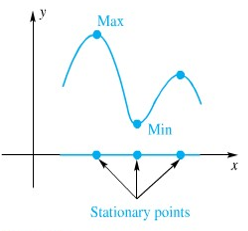
Gambar 5.

Gambar 6.
Ketiga jenis titik ini (titik ujung, titik stasioner, dan titik singular) merupakan titik-titik kunci dari teori maks-min. Sebarang titik dalam daerah asal fungsi \(f\) yang termasuk salah satu dari tiga tipe ini disebut sebuah titik kritis \(f\).
CONTOH 1
Cari titik-titik kritis dari \(f(x)=-2x^3+3x^2\) pada \([-1/2,2]\).
Penyelesaian:
Titik-titik ujung adalah -1/2 dan 2. Untuk mencari titik stasioner kita pecahkan \(f'(x)=-6x^2+6x=0\) untuk \(x\), diperoleh 0 dan 1. Tidak terdapat titik-titik singular. Jadi titik-titik kritis adalah \(-1/2,0,1,2\).
TEOREMA B: Teorema Titik Kritis
Andaikan \(f\) terdefinisi pada selang \(I\) yang memuat titik \(c\). Jika \(f(c)\) adalah nilai ekstrim, maka \(c\) haruslah suatu titik kritis; yaitu \(c\) berupa salah satu:
- titik ujung dari \(I\);
- titik stasioner \(f\); yaitu, titik di mana \(f'(c)=0\); atau
- titik stasioner \(f\); yaitu, titik di mana \(f'(c)\) tidak ada.
Mengingat teorema A dan B, sekarang kita dapat menyatakan suatu prosedur yang sangat sederhana untuk menghitung nilai maksimum atau nilai minimum suatu fungsi kontinu \(f\) pada selang tertutup \(I\).
Langkah 1. Carilah titik-titik kritis dari \(f\) pada \(I\).
Langkah 2. Hitunglah \(f\) pada setiap titik kritis. Yang terbesar adalah nilai maksimum; yang terkecil adalah nilai minimum.
CONTOH 2
Carilah nilai-nilai maksimum dan minimum dari \(f(x)=-2x^3+3x^2\) pada \([-1/2,2]\).
Penyelesaian:
Dalam contoh 1, kita kenali \(-1/2, 0, 1, 2\) sebagai titik-titik kritis. Sekarang \(f(-1/2)=1,f(0)=0,f(1)=1\), dan \(f(2)=-4\). Jadi, nilai maksimum adalah 1 (dicapai pada -1/2 dan 1) dan nilai minimum adalah \(- 4\) (dicapai pada 2). Grafik \(f\) diperlihatkan dalam Gambar 7.

Gambar 7.
CONTOH 3
Fungsi \(F(x)=x^{2/3}\) kontinu di mana-mana. Cari nilai-nilai maksimum dan minimum pada \([-1,2]\).
Penyelesaian:
\(F'(x)=2/3 x^{-1/3}\), tidak pernah 0. Tetapi, \(F'(0)\) tidak ada, sehingga 0 adalah titik kritis, sama seperti titik-titik ujung – 1 dan 2. Sekarnag \(F(-1)=1,F(0)=0\), dan \(F(2)=\sqrt[3]{4} ≈1,59\). Jadi nilai maksimum adalah \(\sqrt[3]{4} \); nilai minimum adalah 0. Grafik diperlihatkan dalam Gambar 8.

Gambar 8.
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Our prime purpose in this life is to help others. And if you can’t help them, at least don’t hurt them.
