
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Teknik Pengintegralan › Integral Fungsi Rasional - Materi, Contoh Soal dan Pembahasan
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Integral Fungsi Rasional - Materi, Contoh Soal dan Pembahasan
Persoalan mengintegralkan fungsi rasional terletak pada mengintegralkan fungsi rasional sejati. Suatu fungsi dinamakan fungsi rasional sejati jika pangkat pembilang kurang dari pangkat penyebut.
Menurut definisi, suatu fungsi rasional adalah hasil bagi dua fungsi suku banyak (polinom). Sebagai contoh, perhatikan tiga fungsi berikut ini:

Sebelum masuk ke pembahasan lebih lanjut, ada dua istilah yang perlu Anda pahami terlebih dahulu, yakni fungsi rasional sejati dan fungsi rasional tidak sejati.
Fungsi \(f\) dan \(g\) di atas dinamakan fungsi rasional sejati karena pangkat dari pembilang kurang dari pangkat penyebut. Sebaliknya, fungsi \(h\) adalah fungsi rasional tidak sejati karena pangkat pembilang lebih besar dari pangkat penyebut.
Fungsi rasional tidak sejati selalu dapat ditulis sebagai jumlah dari fungsi suku banyak dan fungsi rasional sejati. Sebagai contoh, perhatikan berikut ini:

Hasil di atas kita peroleh dengan melakukan pembagian pembilang oleh penyebut, seperti dapat dilihat pada perhitungan berikut.

Oleh karena fungsi suku banyak mudah diintegralkan, maka persoalan mengintegralkan fungsi rasional terletak pada persoalan mengintegralkan fungsi rasional sejati. Tetapi apakah fungsi rasional sejati selalu dapat diintegralkan? Dalam teori, jawabannya selalu dapat, walaupun pencariannya tidak selalu mudah.
Sebagai contoh kita akan mengerjakan integral dari fungsi \(f\) dan \(g\) di atas.
CONTOH 1:
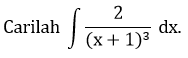
Penyelesaian:
Dengan mengggunakan substitusi \(u=x+1\), maka

CONTOH 2:

Penyelesaian:
Pikirkan dahulu substitusi \(u=x^2-4x+8\) sehingga \(du=(2x-4) \ dx\). Kemudian kita peroleh,

Dalam integral kedua, buatlah menjadi kuadrat murni, sebagai berikut.

Dengan demikian, kita peroleh

Penjabaran Menjadi Pecahan Parsial (Faktor Linear).
Anda mungkin sering menjumlahkan dua pecahan. Misalnya,
\begin{aligned} \frac{2}{x-1} + \frac{3}{x+1} &= \frac{2(x+1) + 3(x-1)}{(x-1)(x+1)} \\[8pt] &= \frac{5x-1}{x^2-1} \end{aligned}
Namun, untuk mengintegralkan fungsi rasional, yang hendak kita pelajari ialah pengerjaan yang sebaliknya yaitu menjabarkannya menjadi pecahan parsial. Sebagai contoh, untuk mengintegralkan fungsi \( \displaystyle f(x) = \frac{5x-1}{x^2-1} \), kita perlu menjabarkan fungsi \( f(x) \) menjadi pecahan parsialnya terlebih dahulu, yakni:
\[ \frac{5x-1}{x^2-1} = \frac{2}{x-1} + \frac{3}{x+1} \]
Dengan demikian, integralnya yaitu:
\begin{aligned} \int \frac{5x-1}{x^2-1} dx &= \int \left( \frac{2}{x-1} + \frac{3}{x+1} \right) dx \\[8pt] &= 2 \ln |x-1| + 3 \ln |x+1| + C \end{aligned}
CONTOH 3: Faktor linear yang berlainan
Jabarkanlah fungsi \((3x-1)/(x^2-x-6)\) menjadi pecahan parsial dan kemudian hitunglah integralnya.
Penyelesaian:
Oleh karena \(x^2-x-6=(x+2)(x-3)\) maka penjabaran pecahan tersebut dapat ditulis dalam bentuk

Tugas kita sekarang ialah menentukan A dan B sehingga (1) menjadi suatu kesamaan. Untuk ini kita hilangkan pecahan, sehingga kita memperoleh

atau; dengan kesetaraan (ekivalensi);
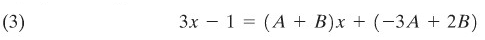
Perhatikan persamaan (3) yang mana akan bernilai benar jika dan hanya jika koefisien dengan pangkat yang sama di ruas kiri dan ruas kanan adalah sama, maka

Dari dua persamaan tersebut kita peroleh \(A=7/5\) dan \(B=8/5\). Sehingga
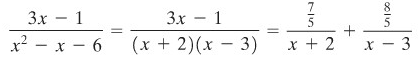
Dengan demikian,

CONTOH 4: Faktor Linear Berganda
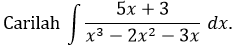
Penyelesaian:
Kita bisa memfaktorkan penyebut dari fungsi dalam soal ini menjadi \(x(x+1)(x-3)\). Karena itu kita dapat menuliskan berikut ini:
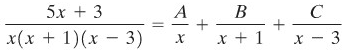
Di sini kita akan mencari nilai A, B, dan C sehingga persamaan di atas bernilai benar. Karena penyebut persamaan ruas kanan dan kirinya adalah sama, maka kita hanya perlu memerhatikan pembilangnya saja, yakni:

Jika kita substitusikan nilai \(x=0, x=-1\) dan \(x=3\), kita peroleh hasil berikut:

atau \(A=-1,B=-1/2,C=3/2\). Dengan demikian, kita dapatkan hasil berikut:

CONTOH 5: Faktor Linear yang Berulang

Penyelesaian:
Untuk kasus faktor linear yang berulang, maka penjabaran menjadi pecahan parsialnya, yaitu:

Tugas kita sekarang adalah mencari nilai A dan B. Setelah penyebut-penyebut dihilangkan kita peroleh hasil berikut:

Selanjutnya, jika kita substitusikan dengan nilai yang sesuai, misalnya \(x = 3\) dan nilai \(x\) sebarang lainnya, misalnya \(x = 0\), kita dapatkan nilai \(B = 3\) dan \(A = 1\). Dengan demikian,
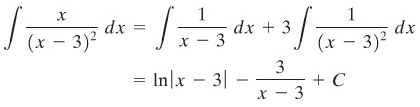
CONTOH 6: Ada beberapa faktor linear berbeda, dan ada yang berulang

Penyelesaian:
Untuk penyebut yang terdiri dari faktor linear berbeda dan ada yang berulang, maka kita jabarkan pemecahan integran dengan cara berikut.

Setelah penyebutnya dihilangkan, kita peroleh
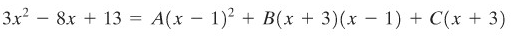
Dengan substitusi \(x = 1, x = -3\), dan \(x = 0\), kita peroleh \(C = 2, A = 4\), dan \(B = -1\). Sehingga
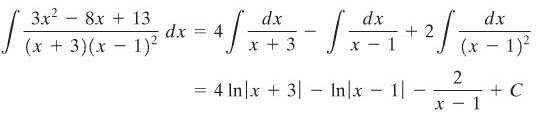
Perhatikan bahwa ada dua pecahan yang berbentuk \(B(x-1)\) dan \(C/(x-1)^2\) dalam penjabaran di atas. Aturan umumnya adalah sebagai berikut. Untuk tiap faktor \((ax+b)^k\) dalam penyebut, ada \(k\) suku dalam penjabaran pecahan parsial, yaitu

Penjabaran Menjadi Pecahan Parsial (Faktor Kuadrat)
Dalam memfaktorkan penyebut suatu pecahan kemungkinan ada faktor kuadrat, misalnya \(x^2+1\), yang tak dapat lagi diuraikan menjadi faktor-faktor linear tanpa mengenalkan bilangan kompleks.
CONTOH 7: Faktor kuadrat tunggal
Jabarkan pecahan berikut menjadi jumlah pecahan parsial,

Kemudian tentukan integralnya.
Penyelesaian:
Kita tulis pecahan tersebut sebagai
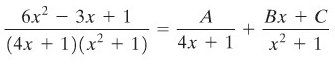
Untuk menentukan konstanta A, B, dan C kita kalikan ruas kiri dan ruas kanan dengan \((4x^2+1)(x^2+1)\). Sehingga kita memperoleh

Apabila kita ambil \(x = -1/4, x = 0\), dan \(x = 1\), kita mendapat

Dengan demikian,

CONTOH 8: Faktor kuadrat berulang
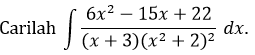
Penyelesaian:
Untuk faktor kuadrat berulang, penjabarannya yaitu

Setelah kita lakukan perhitungan seperlunya, kita akan memperoleh \(A = 1, B = -1, C = 3, D = -5\), dan \(E = 0\). Sehingga

IKHTISAR:
Untuk menjabarkan sebuah fungsi rasional \(f(x)=p(x)/q(x)\) menjadi jumlah pecahan parsial, kita perlu melakukan langkah-langkah sebagai berikut.
Langkah 1
Apabila \(f(x)\) tak sejati, yaitu apabila derajat \(p(x)\) paling sedikit sama dengan derajat \(q(x)\), bagilah terlebih dahulu \(p(x)\) dengan \(q(x)\). Kita akan memperoleh
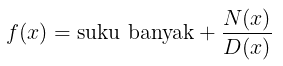
Langkah 2
Uraikan \(D(x)\) menjadi hasilkali faktor-faktor linear dan kuadrat yang tak dapat lagi diuraikan menjadi faktor-faktor linear dengan koefisien riil. Menurut suatu teorema dalam aljabar hal ini selalu mungkin.
Langkah 3
Untuk tiap faktor yang berbentuk \((ax+b)^k\), penjabaran mungkin berbentuk

Langkah 4
Untuk tiap faktor yang berbentuk \((ax^2+bx+c)^m\), penjabaran mungkin menjadi

Langkah 5
Samakan \(N(x)/D(x)\) dengan jumlah semua suku yang diperoleh dalam Langkah ke 3 dan ke 4. Banyaknya konstanta yang harus ditentukan harus sama dengan derajat penyebut, yaitu \(D(x)\).
Langkah 6
Kalikan ruas kiri dan kanan persamaan yang diperoleh dalam Langkah 5 dengan \(D(x)\). Kemudian tentukan konstanta yang harus dicari. Ini dapat diperoleh dengan dua cara: (1) Samakan koefisien dari suku yang derajatnya sama, (2) Substitusikanlah nilai-nilai (yang sesuai) tertentu dalam variabel \(x\).
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Tak peduli bagaimana kerasnya kehidupanmu di masa lalu, kamu selalu bisa memulainya lagi.
