www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Turunan Fungsi › Definisi Turunan
Definisi Turunan
Banyak fenomena dalam dunia nyata yang melibatkan perubahan kuantitas seperti kecepatan roket, inflasi mata uang, jumlah bakteri dalam suatu kultur, dan sebagainya. Fenomena-fenomena tersebut sering kali dapat dijelaskan dengan menggunakan konsep turunan.
Banyak fenomena dalam dunia nyata yang melibatkan perubahan kuantitas seperti kecepatan roket, inflasi mata uang, jumlah bakteri dalam suatu kultur, intensitas goncangan gempa bumi, tegangan sinyal listrik, dan sebagainya.
Fenomena-fenomena tersebut sering kali dapat dijelaskan dengan menggunakan konsep turunan atau derivatif, yakni alat matematika untuk mempelajari tingkat perubahan satu kuantitas relatif terhadap yang lain.
Kita akan mulai penjelasan dengan memberikan definisi dari turunan terlebih dahulu. Untuk mamahami definisi turunan, anda perlu mengenal konsep limit. Jika anda belum paham mengenai materi limit, anda tidak perlu khawatir. Di website ini kami telah menyediakan materi tersebut.
Apabila fungsi \(f(x)\) mempunyai turunan untuk setiap \(x\) anggota domain \(D\), dengan \(D∈R\) (bilangan real) maka diperoleh turunan fungsi dari \(f(x)\) yang dirumuskan:

Perhatikan bahwa \( f'(x) \) menyatakan turunan dari fungsi \(f(x)\). Untuk lebih jelasnya, kita nyatakan dalam definisi berikut:
DEFINISI:
Turunan fungsi \(f\) adalah fungsi lain \(f'\) (dibaca “\(f\) aksen”) yang nilainya pada sebarang bilangan \(x\) adalah

asalkan limit ini ada.
Jika limit pada definisi di atas memang ada, maka dikatakan bahwa \(f\) terdiferensialkan (terturunkan) di \(x\). Pencarian turunan disebut pendiferensialan; bagian kalkulus yang berhubungan dengan turunan disebut kalkulus diferensial.
CONTOH 1:
Andaikan \(f(x)= 13x - 6\). Cari \(f'(4)\).
Penyelesaian:

CONTOH 2:
Jika \(f(x) = x^3 + 7x\). Cari \(f'(x)\).
Penyelesaian:

CONTOH 3:
Jika \(f(x) = 1/x\), cari \(f'(x)\)
Penyelesaian:

Jadi, \(f'(x) = -1/x^2\) dengan daerah asalnya adalah semua bilangan riil kecuali \(x = 0\).
CONTOH 4:
Cari turunan dari \(F\) jika \(F(x) = √x, x > 0\).
Penyelesaian:

Dalam contoh kita sejauh ini, pencarian turunan selalu menyangkut pengambilan limit suatu hasilbagi di mana pembilang dan penyebut keduanya menuju nol. Lalu kita menyederhanakan hasilbagi ini sehingga kita dapat mencoret faktor \(h\) dari pembilang dan penyebut, dengan demikian memungkinkan kita untuk menghitung limit.
Dalam contoh yang sekarang, hal ini dapat dilakukan dengan merasionalkan pembilang.

Jadi, \(F'(x) = 1/2\sqrt{x}\) dengan daerah asalnya adalah \((0, ∞)\).
Bentuk-Bentuk yang Setara untuk Turunan
Tidak ada aturan yang mengharuskan pemakaian huruf \(h\) dalam mendefinisikan \(f'(c)\). Dengan kata lain, kita bisa memakai huruf lain yang diinginkan. Sebagai contoh, kita bisa menggunakan huruf \(p, s\) atau huruf lainnya, seperti terlihat berikut ini:
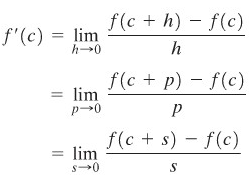
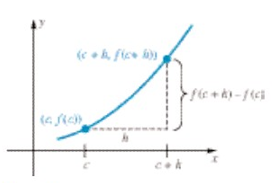
Gambar 1

Gambar 2
Perubahan yang lebih radikal, tetapi masih tetap hanya suatu perubahan cara penulisan, mungkin mudah dipahami dengan membandingkan Gambar 1 dan Gambar 2. Perhatikan bagaimana \(x\) mengambil tempat \(c + h\), sehingga \(x - c\) menggantikan \(h\). Jadi,

Dalam nada yang serupa, kita boleh menuliskan
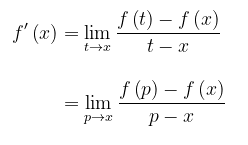
CONTOH 5:
Gunakan hasil dalam kotak berwarna biru di atas untuk mencari \(g'(c)\), jika \(g(x) = 2/(x + 3)\).
Penyelesaian:

Di sini kita memanipulasikan hasilbagi sampai kita dapat mencoret suatu faktor \(x - c\) dari pembilang dan penyebut. Kemudian kita dapat menghitung limit tersebut.
CONTOH 6:
Masing-masing yang berikut adalah suatu turunan, tetapi dari fungsi apa dan di titik mana?
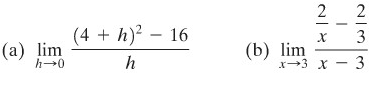
Penyelesaian:
a. Ini adalah turunan dari \(f(x) = x^2\) di \(x = 4\)
b. Ini adalah turunan dari \(f(x) = 2/x\) di \(x = 3\).
Keterdiferensialan Menunjukkan Kekontinuan
TEOREMA A:
Jika \(f'(c)\) ada, maka \(f\) adalah kontinu di \(c\).
Bukti:
Kita perlu menunjukkan bahwa
\[ \lim_{x\to c} f(x) = f(c) \]
Sekarang

Sehingga,
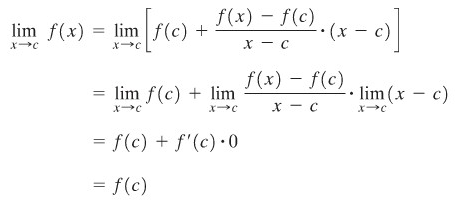
Kebalikan dari teorema A adalah tidak benar, yakni jika fungsi \(f\) kontinu di \(c\), maka tidak berarti \(f\) mempunyai turunan di \(c\). Ini dengan mudah dapat dilihat dengan memandang \(f(x) = |x|\) di titik asal (Gambar 3). Fungsi ini pasti kontinu di nol, tetapi tidak mempunyai turunan di sana. Kenapa bisa demikian? Perhatikalah bahwa
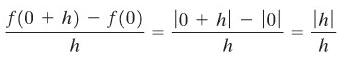
Limit ini tidak ada karena limit kanan tidak sama dengan limit kiri.

Sedangkan,
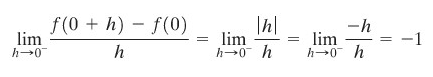
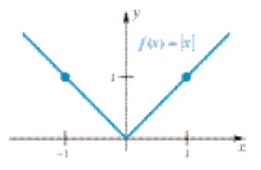
Gambar 3
Argumentasi yang baru disajikan memperlihatkan bahwa di sebarang titik di mana fungsi mempunyai sebuah sudut yang tajam, maka fungsi penyebut kontinu tetapi tidak terdiferensialkan. Grafik dalam Gambar 4 menunjukkan sejumlah kemungkinan.
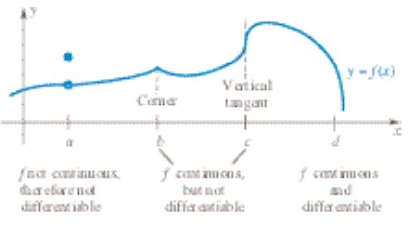
Gambar 4
Kita tegaskan dalam Gambar 4 bahwa turunan tidak ada di titik \(c\) di mana garis singgungnya tegak (vertikal). Ini disebabkan
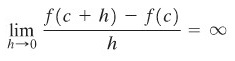
Hal ini berkaitan dengan kenyataan bahwa kemiringan suatu garis vertikal tak terdefinisi.
Increment dan Notasi Leibniz untuk turunan
Terdapat notasi lain untuk menyatakan turunan yang disebut notasi Leibniz. Notasi ini cukup populer dan sering dijumpai dalam penulisan sejumlah buku. Oleh karena itu, kita akan mempelajarinya di sini. Tetapi sebelum itu kita perlu mengenal apa yang disebut dengan increment.
Lalu apa itu increment? Jika nilai sebuah variabel \(x\) berubah dari \(x_1\) ke \(x_2\), maka \(x_2 - x_1\) (perubahan dalam \(x\)) disebut increment \(x\) dan biasanya dinyatakan dengan \(Δx\) (dibaca “delta \(x\)”). Perhatikan bahwa \(Δx\) tidak berarti \(Δ\) kali \(x\). Jika \(x_1 = 4.1\) dan \(x_2 = 5.7\), maka

Jika \(x_1 = c\) dan \(x_2 = c + h\), maka

Selanjutnya anggaplah bahwa \(y = f(x)\) menentukan sebuah fungsi. Jika \(x\) berubah dari \(x_1\) ke \(x_2\), maka \(y\) berubah dari \(y_1 = f(x_1)\) ke \(y_2 = f(x_2)\). Dengan demikian, berkaitan dengan increment \(Δx = x_2 - x_1\) dalam \(x\), terdapat increment dalam \(y\) yang diberikan oleh

CONTOH 7:
Misalkan \(y = f(x) = 2 - x^2\). Cari \(Δy\) saat \(x\) berubah dari 0,4 ke 1.3 (lihat Gambar 5).
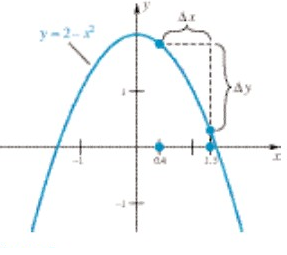
Gambar 5
Penyelesaian:
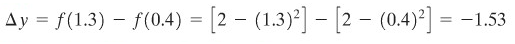
Setelah kita paham mengenai increment, sekarang kita siap dengan notasi Leibniz untuk turunan. Pertama, anggaplah bahwa variabel independen berubah dari \(x\) menjadi \(x + Δx\). Perubahan yang bersesuaian dengan variabel dependen, \(y\), akan menjadi
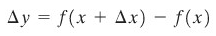
dan rasio

merepsentasikan kemiringan garis secant melalui \((x, f(x))\), seperti ditunjukkan pada Gambar 6. Ketika \(Δx → 0\), kemiringan dari garis secant ini mendekati garis singgung, dan untuk kemiringan terakhir ini, kita gunakan simbol \(dy/dx\) yang merupakan notasi Leibniz untuk turunan. Dengan demikian,
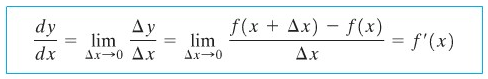
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
It always sems impossible until it's done.
