www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Aplikasi Turunan › Garis Singgung
Garis Singgung
Studi mengenai turunan terkait erat dengan konsep geometri untuk garis singgung suatu kurva. Oleh karena itu, kita akan membahas definisi umum garis singgung dan metode untuk menemukan kemiringan dan persamaannya menggunakan konsep turunan.
Studi mengenai turunan terkait erat dengan konsep geometri untuk garis singgung suatu kurva. Oleh karena itu, kita akan membahas definisi umum garis singgung dan metode untuk menemukan kemiringan dan persamaannya menggunakan konsep turunan.
Perhatikan grafik dari persamaan \(y=f(x)\) pada Gambar 1. Titik \(P\) mempunyai koordinat \((c,f(c))\), titik \(Q\) di dekatnya mempunyai koordinat \((c+h,f(c+h))\), dan talibusur yang melalui \(P\) dan \(Q\) mempunyai kemiringan \(m_{sec}\) yang diberikan oleh


Gambar 1
Dengan menggunakan konsep limit, yang mana telah kita pelajari pada bagian sebelumnya, sekarang kita bisa memberikan definisi yang formal untuk garis singgung.
DEFINISI:
Garis singgung kurva \(y=f(x)\) di titik \(P(c,f(c))\) adalah garis yang melalui titik \(P\) dengan kemiringan
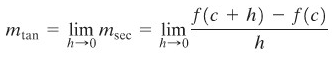
asalkan bahwa limit ini ada dan bukan \(∞\) atau \(-∞\).
CONTOH 1:
Cari kemiringan garis singgung pada kurva \(y=f(x)=x^2\) di titik (2, 4).
Pembahasan:
Garis yang kemiringannya kita cari diperlihatkan pada Gambar 2. Jelas ia mempunyai suatu kemiringan positif yang besar.
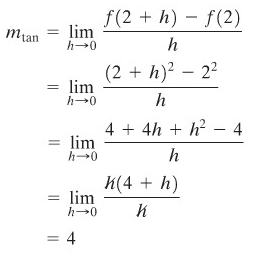

Gambar 2
CONTOH 2:
Cari kemiringan garis singgung pada kurva \(y=f(x)=-x^2+2x+2\) pada titik-titik yang koordinat-x nya -1, 1/2, 2, dan 3.
Pembahasan:
Ketimbang membuat empat perhitungan terpisah, kelihatannya lebih bijaksana untuk menghitung kemiringan itu di titik yang koordinat-x nya di titik c dan kemudian mendapatkan empat jawaban yang diinginkan dengan cara substitusi.
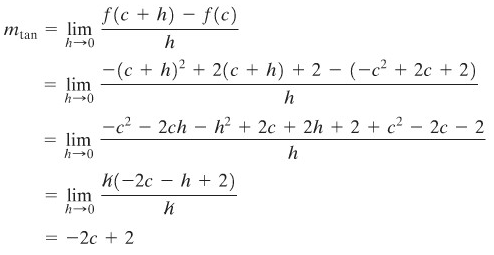
Keempat kemiringan yang diinginkan (diperoleh dengan menetapkan \(c=-1,1/2,2\), dan \(3\)) adalah \(4, 1, -2,\) dan \(-4\). Jawaban ini memang bersesuaian dengan grafik pada Gambar 3.
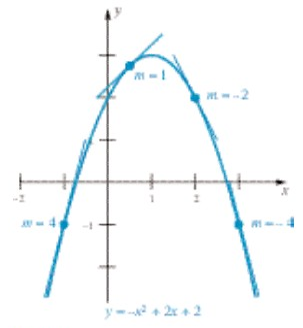
Gambar 3
CONTOH 3:
Cari persamaan garis singgung pada kurva \(y=1/x\) di titik \((2,1/2)\) (lihat gambar 4)

Gambar 4
Pembahasan:

Dengan mengetahui kemiringan garis \((m = -1/4)\) dan titik \((2, 1/2)\) pada garis itu, secara mudah kita dapat menuliskan persamaannya dengan memakai bentuk kemiringan titik \(y-y_0=m(x-x_0)\). Hasilnya adalah \(y-1/2=-1/4(x-2)\), atau ekuivalen dengan, \(y=1-1/4 x\).
CONTOH 4:
Cari persamaan garis singgung pada grafik \(y=3 \sin{2x}\) di titik \((π/2,0)\) (lihat gambar 5).
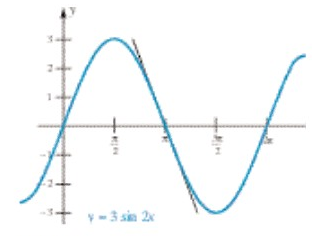
Gambar 5
Pembahasan:
Kita memerlukan turunan dari \(\sin{2x}\); sayangnya, kita hanya tahu bagaimana mencari turunan dari \(\sin{x}\). Tetapi, \(\sin{2x} = 2 \sin{x} \cos{x}\). Jadi,

Pada \(x=π/2\), turunan ini bernilai \(-6\), yang karena itu merupakan kemiringan garis singgung yang diinginkan. Persamaan garis ini adalah
\[ y-0 = -6(x-\frac{\pi}{2}) \]
CONTOH 5:
Cari persamaan garis singgung pada kurva \(y^3-xy^2+\cos{xy}=2\) di titik (0,1).
Pembahasan:
Untuk penyederhanaan, kita gunakan notasi \(y'\) ketimbang \(dy/dx\). Jika kita mendiferensialkan kedua ruas dan menyamakan hasilnya, kita peroleh

Di titik \((0,1), \ y’ = 1/3\). Sehingga, persamaan garis singgung di \((0,1)\) adalah

atau
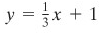
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
There is always inequality in life. Some men are killed in a war and some men are wounded and some men never leave the country. Life is unfair.
