www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Teknik Pengintegralan › Aturan ILATE dalam Integral Parsial
Aturan ILATE dalam Integral Parsial
Menurut Aturan ILATE, dalam teknik integral parsial, fungsi yang akan dimisalkan sebagai u mengikuti urutan berikut: Invers, Logaritma, Aljabar, Trigonometri, dan Eksponensial.
Kita telah mempelajari beberapa teknik untuk menyelesaikan integral: teknik integral substitusi, teknik integral substitusi trigonometri, teknik integral parsial, dan lainnya.
Dalam teknik integral parsial terdapat sebuah aturan penting yang dikenal dengan Aturan ILATE. Aturan ini sangat berguna untuk mempermudah penggunaan teknik integral parsial. Kita akan mempelajarinya secara jelas di artikel ini.
Sebagaimana kita ketahui, rumus dari teknik integral parsial yaitu:
\[ \int u \ dv = uv - \int v \ du \]
Jika integralnya ada batas atau disebut integral tertentu, maka rumus integral parsialnya menjadi
\[ \int_a^b u \ dv = [uv]_a^b - \int_a^b v \ du \]
Dari rumus di atas, kita tahu bahwa integral parsial dapat digunakan untuk mengintegralkan perkalian dua fungsi. Untuk menggunakan teknik ini, kita perlu melakukan pemisalan \(u\) dan \(dv\). Biasanya kita akan memisalkan \(u\) yang apabila fungsinya diturunkan akan menuju nol dan \(dv\) sebagai fungsi yang mudah untuk diintegralkan. Untuk lebih jelasnya perhatikan contoh berikut:
CONTOH 1:
Selesaikan \( \displaystyle \int x \ \cos x \ dx \) menggunakan rumus integral parsial.
Pembahasan:
Untuk menyelesaikan soal ini, kita akan gunakan teknik integral parsial. Misalkan \(u = x\) dan \(dv = \cos x \ dx\) sehingga diperoleh
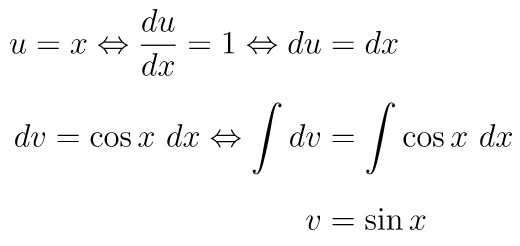
Dengan substitusi hasil yang kita dapatkan di atas ke rumus integral parsial, kita peroleh berikut ini:

Dalam Contoh 1 di atas, Anda mungkin bertanya apakah ada ketentuan dalam penentuan \(u\) dan \(dv\)? Misalnya mengapa kita misalkan \(u = x\) dan \(dv = \cos x \ dx\). Mengapa tidak sebaliknya, misalnya \(u = \cos x\) dan \(dv = x \ dx\)? Apakah ada sebuah aturan baku yang bisa dipakai secara umum?
Untuk menjawab ini, sebuah aturan penting telah diperkenalkan yaitu Aturan ILATE. Menurut aturan ini, fungsi yang akan dimisalkan sebagai \(u\) mengikuti urutan berikut:
I: Fungsi Invers
L: Fungsi Logaritma
A: Fungsi Aljabar
T: Fungsi Trigonometri
E: Fungsi Eksponensial
Singkatnya, menurut Aturan ILATE, dalam teknik integral parsial fungsi dalam integral yang akan dimisalkan sebagai \(u\) mengikuti urutan di atas yakni: Invers, Logaritma, Aljabar, Trigonometri, dan Eksponensial.
Dengan kata lain, apabila fungsi dalam integralnya merupakan perkalian antara fungsi invers trigonometri dan logaritma, maka kita akan misalkan fungsi invers trigonometri tersebut sebagai \(u\) dan fungsi logaritmanya sebagai \(dv\). Apabila fungsi dalam integral berupa fungsi aljabar dan trigonometri, maka kita misalkan fungsi aljabarnya sebagai \(u\) dan fungsi trigonometrinya sebagai \(dv\).
CONTOH 2:
Selesaikan \( \displaystyle \int \sin^{-1} x \ dx \).
Pembahasan:
Untuk menyelesaikan integral ini, kita bisa gunakan teknik integral parsial. Pertama, kita perlu melakukan pemisalan \(u\) dan \(dv\). Berdasarkan Aturan ILATE, fungsi yang akan dimisalkan sebagai \(u\) mengikuti urutan berikut: Invers, Logaritma, Aljabar, Trigonometri, dan Eksponensial.
Dengan demikian, fungsi invers trigonometri \(\sin^{-1} x\) akan dimisalkan sebagai \(u\) atau \(u = \sin^{-1}x\) dan \(dv = dx\). Dari pemisalan \(u\) dan \(dv\), kita peroleh:
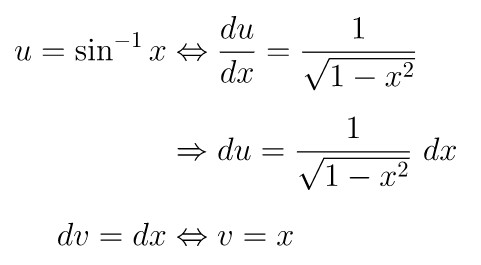
Selanjutnya, dengan substitusi hasil yang kita peroleh di atas ke rumus integral parsial, kita dapatkan berikut ini:

CONTOH 3:
Selesaikan \( \displaystyle \int x \ \sin^{-1} x \ dx \).
Pembahasan:
Perhatikan bahwa fungsi dalam integral ini merupakan perkalian antara fungsi aljabar dan fungsi invers trigonometri. Integral ini dapat diselesaikan menggunakan teknik integral parsial sehingga kita perlu melakukan pemisalan u dan dv terlebih dahulu.
Ingat bahwa berdasarkan Aturan ILATE, fungsi yang akan dimisalkan sebagai u mengikuti urutan berikut: Invers, Logaritma, Aljabar, Trigonometri, dan Eksponensial. Oleh karena itu, fungsi invers trigonometri \(\sin^{-1}x\) akan dimisalkan sebagai \(u\) dan \(x \ dx\) sebagai \(dv\), atau bisa kita tuliskan:

Dari pemisalan u dan dv di atas, kita peroleh:

Selanjutnya, dengan substitusi hasil yang diperoleh di atas ke rumus integral parsial, kita dapatkan hasil berikut:
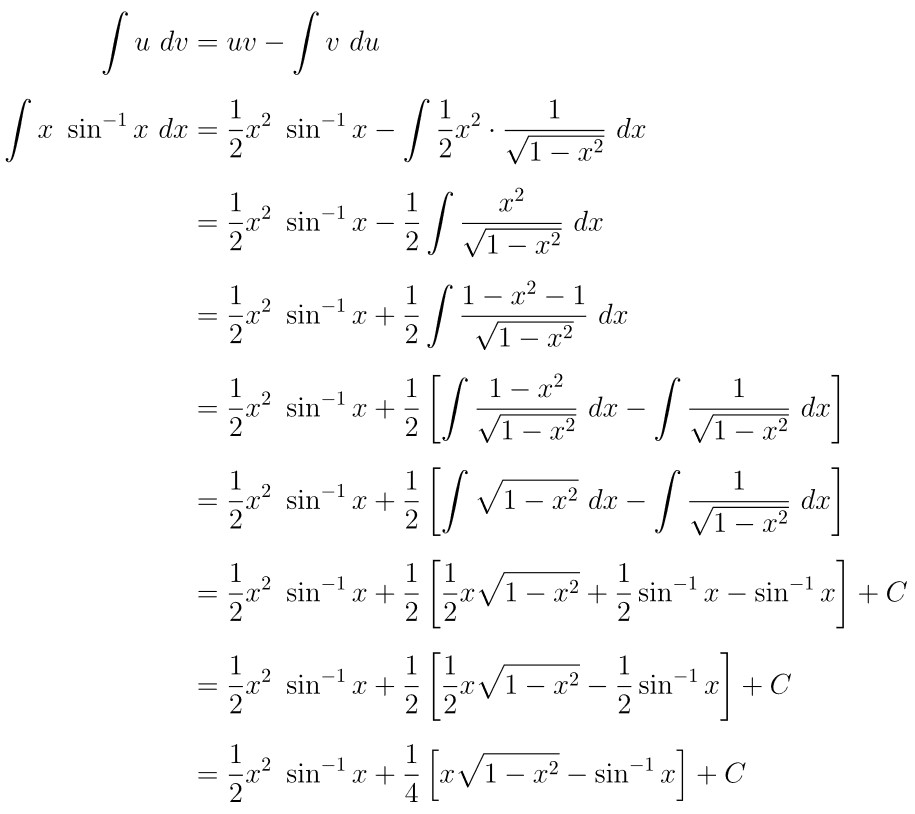
CONTOH 4:
Selesaikan \( \displaystyle \int x \ \tan^{-1} x \ dx \).
Pembahasan:
Integral ini dapat diselesaikan menggunakan teknik integral parsial. Dengan mengikuti langkah-langkah dalam Contoh 3, kita peroleh pemisalan \(u=\tan^{-1} x\) dan \(dv = x \ dx\).
Dengan demikian, kita dapatkan hasil berikut:

Selanjutnya, dengan substitusi hasil yang diperoleh di atas ke rumus integral parsial, kita dapatkan hasil berikut:

CONTOH 5:
Selesaikan \( \displaystyle \int x \ \ln x \ dx \).
Pembahasan:
Perhatikan bahwa fungsi dalam integral ini merupakan perkalian antara fungsi aljabar dan fungsi logaritma natural. Integral ini dapat diselesaikan menggunakan teknik integral parsial sehingga kita perlu melakukan pemisalan u dan dv.
Menurut Aturan ILATE, fungsi yang akan dimisalkan sebagai u mengikuti urutan berikut: Invers, Logaritma, Aljabar, Trigonometri, dan Eksponensial. Oleh karena itu, fungsi yang akan dimisalkan sebagai u yaitu fungsi logaritma natural yakni \(u = \ln x\) dan fungsi aljabarnya akan dimisalkan sebagai dv, yakni \(dv = x \ dx\), atau dapat kita tuliskan menjadi:
\[ u = \ln x \quad \text{dan} \quad dv = x \ dx \]
Dengan demikian, kita peroleh berikut ini:

Dari hasil di atas, sekarang kita dapat selesaikan integral pada soal yaitu:

CONTOH 6:
Selesaikan \( \displaystyle \int x^n \ \ln x \ dx \).
Pembahasan:
Fungsi dalam integral ini merupakan perkalian antara fungsi aljabar dan fungsi logaritma natural. Adapun langkah-langkah penyelesaian dari integral ini dapat mengikuti Contoh 5 di atas. Kita misalkan \(u = \ln x\) dan \(dv = x^n \ dx\) sehingga kita peroleh:

Dari hasil di atas, sekarang kita dapat selesaikan integral pada soal yaitu:

CONTOH 7:
Selesaikan \( \displaystyle \int e^x \ \sin x \ dx \).
Pembahasan:
Perhatikan bahwa fungsi dalam integral ini merupakan perkalian antara fungsi eksponensial dan trigonometri sehingga berdasarkan Aturan ILATE, fungsi trigonometrinya akan dimisalkan sebagai u yakni \(u = \sin x\) dan fungsi eksponensialnya sebagai dv, yakni \(dv = e^x \ dx\).
Dengan demikian, kita peroleh:

Selanjutnya dari hasil di atas, kita peroleh berikut ini:

Untuk melanjutkan hasil di atas, kita perlu menyelesaikan \(\int e^x \cos x \ dx\) terlebih dahulu. Kita bisa selesaikan integral tersebut menggunakan teknik integral parsial dengan memisalkan \(u = e^x\) dan \(dv = \cos x \ dx\) sehingga kita dapatkan berikut ini:
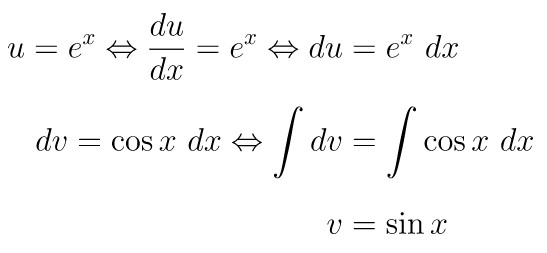
Dengan melanjutkan hasil yang kita peroleh sebelumnya kita peroleh jawaban dari integral pada soal, yaitu:

CONTOH 8:
Selesaikan \( \displaystyle \int e^x \ \cos x \ dx \).
Pembahasan:
Sama dengan kasus pada Contoh 7 di atas, kita misalkan \(u = \cos x\) dan \(dv = e^x \ dx\), sehingga kita peroleh:

Selanjutnya dari hasil di atas, kita peroleh berikut ini:

Untuk melanjutkan hasil di atas, kita perlu menyelesaikan \(\int e^x \sin x \ dx\) terlebih dahulu. Kita bisa selesaikan integral tersebut menggunakan teknik integral parsial dengan memisalkan \(u = \sin x\) dan \(dv = e^x \ dx\) sehingga kita dapatkan berikut ini:

Dengan melanjutkan hasil yang kita peroleh sebelumnya kita peroleh jawaban dari integral pada soal, yaitu:

CONTOH 9:
Selesaikan \( \displaystyle \int x \ \sin x \ dx \).
Pembahasan:
Perhatikan fungsi dalam integral ini merupakan perkalian antara fungsi aljabar dan trigonometri sehingga berdasarkan Aturan ILATE, kita akan misalkan fungsi aljabarnya sebagai u, yakni \(u = x\) dan fungsi trigonometrinya sebagai dv, yakni \(dv = \sin x \ dx\).
Dengan demikian, kita dapatkkan hasil berikut:

Selanjutnya dari hasil di atas, kita peroleh berikut ini:

CONTOH 10:
Selesaikan \( \displaystyle \int x \ e^x \ dx \).
Pembahasan:
Perhatikan bahwa fungsi dalam integral ini merupakan perkalian antara fungsi aljabar dan eksponesial, sehingga berdasarkan Aturan ILATE, kita misalkan fungsi aljabarnya sebagai u, yakni \(u = x\) dan fungsi eksponensialnya sebagai dv, yakni \(dv = e^x \ dx\).
Dengan demikian, kita dapatkkan hasil berikut:

Selanjutnya dari hasil di atas, kita peroleh berikut ini:
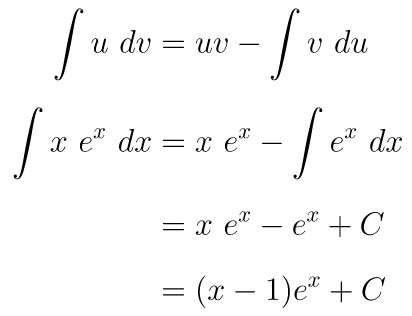
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Do small things with great love.
