Kalkulus I   »   Turunan Fungsi   ›  Turunan Fungsi Trigonometri

Turunan Fungsi Trigonometri

Konsep turunan juga berlaku untuk fungsi trigonometri seperti fungsi sinus, fungsi cosinus, fungsi tangen, dan kebalikan dari masing-masing fungsi tersebut yakni fungsi cosecan, fungsi secan, dan fungsi cotangen.

Pada artikel sebelumnya, kita telah membahas definisi turunan. Sekarang kita akan lanjutkan materi tersebut untuk turunan yang melibatkan fungsi trigonometri seperti fungsi sinus, fungsi cosinus, fungsi tangen, dan kebalikan dari masing-masing fungsi tersebut yakni fungsi cosecan, fungsi secan, dan fungsi cotangen.

Untuk mencari turunan fungsi sinus atau \(D(\sin⁡{x})\), kita bisa menggunakan definisi turunan dan identitas penambahan untuk \(\sin⁡{(x+h)}\).

Perhatikan bahwa dua limit pada dua ekspresi terakhir ini sesungguhnya merupakan limit yang telah kita pelajari pada pembahasan mengenai limit. Dan kita telah membuktikan bahwa

Jadi,

Dengan cara serupa, kita dapat mencari turunan fungsi cosinus yaitu

Kita ringkaskan hasil-hasil ini dalam sebuah teorema penting.

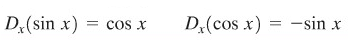
Untuk mencari turunan fungsi tangen atau \(D(\tan⁡{x})\), kita bisa menggunakan definisi turunan dan identitas penambahan untuk \(\tan{(x+h)}\), yakni

Sebenarnya ada cara mudah untuk mencari turunan dari fungsi tangen, yakni kita dapat gunakan kesamaan \( \tan x = \frac{\sin x}{\cos x} \) dan kemudian menerapkan rumus turunan untuk hasilbagi dua fungsi. Misalkan \( u = \sin x \) dan \( v = \cos x \), maka berdasarkan turunan untuk hasilbagi, kita peroleh

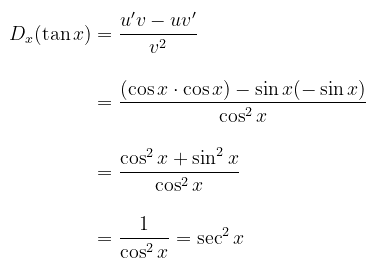
Turunan Fungsi \( \csc x, \sec x \) dan \( \tan x \)

Untuk mencari turunan fungsi \( \csc x, \sec x \) dan \( \tan x \), kita dapat memanfaatkan kesamaan bahwa

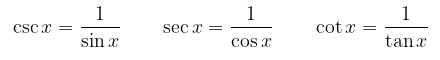
dan kemudian menerapkan rumus turunan untuk hasil bagi dua fungsi seperti yang telah kita contohkan untuk mencari turunan fungsi tangen. Dari hasil perhitungan diperoleh

Perhatikan beberapa contoh soal berikut:

Cukup sekian penjelasan mengenai turunan fungsi trigonometri beserta contoh soal dan pembahasannya dalam artikel ini. Semoga bermanfaat.

Sumber:

Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.

Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.