www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Integral › Integral Invers Trigonometri, Contoh Soal dan Pembahasan
Integral Invers Trigonometri, Contoh Soal dan Pembahasan
Ada banyak soal integral yang melibatkan fungsi invers trigonometri di mana penyelesaiannya bisa menggunakan teknik integral parsial. Pada artikel ini kita akan membahas beberapa contoh soal integral dari fungsi invers trigonometri.
Contoh 1:
Tentukan \( \int \sin^{-1} x \ dx \).
Pembahasan:
Untuk menyelesaikan soal ini kita akan gunakan teknik integral parsial dengan memisalkan \(u = \sin^{-1} x\) dan \(dv = dx\) sehingga kita peroleh berikut ini:

Selanjutnya, berdasarkan informasi yang kita peroleh di atas, maka penyelesaian integral pada soal yaitu:
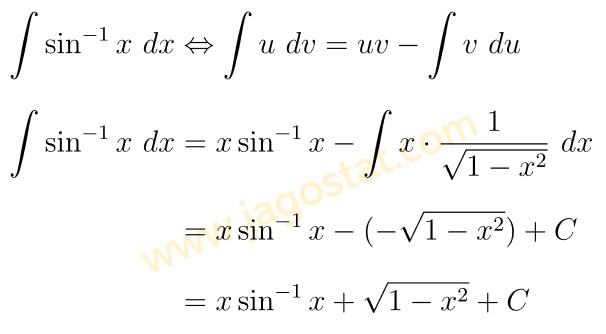
Contoh 2:
Tentukan \( \int x \sin^{-1} x \ dx \).
Pembahasan:
Kita misalkan \(u = \sin^{-1} x\) dan \(dv = x \ dx\) sehingga kita peroleh:

Selanjutnya, dengan substitusi hasil yang diperoleh di atas ke rumus integral parsial, kita dapatkan hasil berikut:

Contoh 3:
Tentukan \( \int \cos^{-1} x \ dx \).
Pembahasan:
Kita misalkan \(u = \cos^{-1} x\) dan \(dv = dx\) sehingga kita peroleh:

Selanjutnya, dengan substitusi hasil yang diperoleh di atas ke rumus integral parsial, kita dapatkan hasil berikut:

Contoh 4:
Tentukan \( \int x \cos^{-1} x \ dx \).
Pembahasan:
Kita misalkan \(u = \cos^{-1} x\) dan \(dv = x \ dx\) sehingga kita peroleh:

Selanjutnya, dengan substitusi hasil yang diperoleh di atas ke rumus integral parsial, kita dapatkan hasil berikut:

Contoh 5:
Tentukan \( \int \tan^{-1} x \ dx \).
Pembahasan:
Integral ini dapat diselesaikan menggunakan teknik integral parsial. Dengan memisalkan \(u=\tan^{-1} x\) dan \(dv = dx\), kita peroleh hasil berikut:

Selanjutnya, dengan substitusi hasil yang diperoleh di atas ke rumus integral parsial, kita dapatkan hasil berikut:
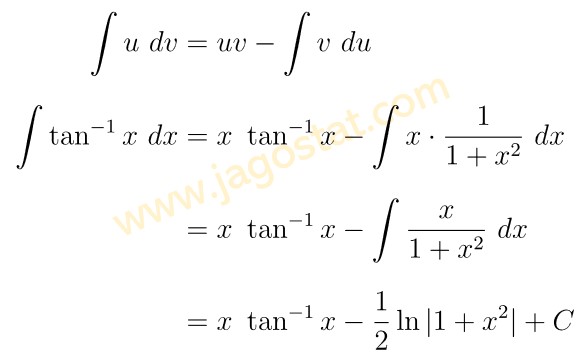
Contoh 6:
Tentukan \( \int x \tan^{-1} x \ dx \).
Pembahasan:
Integral ini dapat diselesaikan menggunakan teknik integral parsial. Dengan memisalkan \(u=\tan^{-1} x\) dan \(dv = x \ dx\) kita peroleh hasil berikut:

Selanjutnya, dengan substitusi hasil yang diperoleh di atas ke rumus integral parsial, kita dapatkan hasil berikut:

Contoh 7:
Tentukan \( \int \csc^{-1} x \ dx \).
Pembahasan:
Integral ini dapat diselesaikan menggunakan teknik integral parsial. Dengan memisalkan \(u=\csc^{-1} x\) dan \(dv = dx\), kita peroleh hasil berikut:
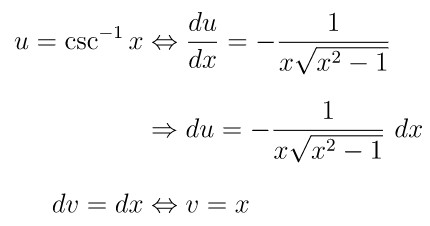
Selanjutnya, dengan substitusi hasil yang diperoleh di atas ke rumus integral parsial, kita dapatkan hasil berikut:

Contoh 8:
Tentukan \( \int \sec^{-1} x \ dx \).
Pembahasan:
Integral ini dapat diselesaikan menggunakan teknik integral parsial. Dengan memisalkan \(u=\sec^{-1} x\) dan \(dv = dx\), kita peroleh hasil berikut:

Selanjutnya, dengan substitusi hasil yang diperoleh di atas ke rumus integral parsial, kita dapatkan hasil berikut:

Contoh 9:
Tentukan \( \int \cot^{-1} x \ dx \).
Pembahasan:
Integral ini dapat diselesaikan menggunakan teknik integral parsial. Dengan memisalkan \(u=\cot^{-1} x\) dan \(dv = dx\), kita peroleh hasil berikut:
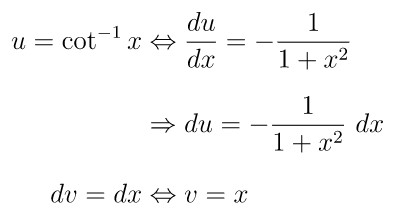
Selanjutnya, dengan substitusi hasil yang diperoleh di atas ke rumus integral parsial, kita dapatkan hasil berikut:

Contoh 10:
Tentukan \( \int x \cot^{-1} x \ dx \).
Pembahasan:
Integral ini dapat diselesaikan menggunakan teknik integral parsial. Dengan memisalkan \(u=\cot^{-1} x\) dan \(dv = dx\), kita peroleh hasil berikut:

Selanjutnya, dengan substitusi hasil yang diperoleh di atas ke rumus integral parsial, kita dapatkan hasil berikut:

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan jika ada yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Inside of every problem lies an opportunity.
