www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Turunan Fungsi › Aturan Pencarian Turunan
Aturan Pencarian Turunan
Proses pencarian turunan suatu fungsi langsung menggunakan definisi turunan selain memakan waktu juga membosankan. Kita akan mengembangkan cara yang akan memungkinkan kita untuk mencari turunan dari fungsi-fungsi yang tampak rumit dengan segera.
Proses pencarian turunan suatu fungsi langsung menggunakan definisi turunan, yakni dengan menyusun hasilbagi selisih

dan menghitung limitnya, memakan waktu dan membosankan. Kita akan mengembangkan cara yang akan memungkinkan kita untuk memperpendek proses yang berkepanjangan ini sehingga memungkinkan kita untuk mencari turunan dari fungsi-fungsi yang tampak rumit dengan segera.
Ingat kembali bahwa turunan suatu fungsi adalah fungsi lain \(f'\). Misalnya, jika \(f(x) = x^2\) adalah rumus untuk \(f\), maka \(f'(x) = 2x\) adalah rumus untuk \(f'\). Pengambilan turunan dari \(f\) (pendiferensialan \(f\)) adalah pengoperasian pada \(f\) untuk menghasilkan \(f'\).
Sering kali kita memakai huruf \(D\) untuk menunjukkan operasi ini. Jadi kita menuliskan \(D_f = f'\), \(D_f(x) = f'(x)\), atau (dalam contoh yang disebutkan di atas) \(D(x^2) = 2x\). Semua teorema di bawah dinyatakan dalam cara penulisan fungsional dan dalam cara penulisan operator \(D\).
Konstanta dan Aturan Pangkat.
TEOREMA A: Aturan Fungsi Konstanta
Jika \(f(x) = k\) dengan \(k\) suatu konstanta, maka untuk sebarang \(x\), \(f'(x) = 0\); yakni
\[ D_x(k) = 0 \]
Bukti:

TEOREMA B: Aturan Fungsi Identitas
Jika \(f(x) = x\), maka \(f'(x) = 1\); yakni
\[ D_x(k) = 1 \]
Bukti:

Teorema kita berikutnya akan berkaitan dengan pencarian turunan dari suatu pangkat. Namun, sebelum itu mari kita ingat sejenak bagaimana memangkatkan suatu binomial. Perhatikan berikut ini:
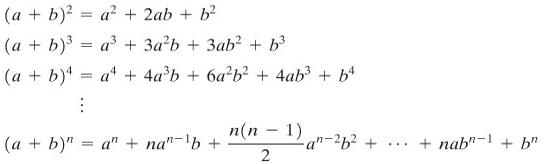
TEOREMA C: Aturan pangkat
Jika \(f(x) = x^n\) dengan \(n\) bilangan-bilangan bulat positif maka \(f'(x) = nx^{n-1}\); yakni
\[ D_x(x^n) = nx^{n-1} \]
Bukti:

Di dalam kurung siku, semua suku kecuali yang pertama mempunyai \(h\) sebagai faktor, sehingga masing-masing suku ini mempunyai limit nol bila \(h\) mendekati nol. Jadi
\[ f'(x) = nx^{n-1} \]
Sebagai ilustrasi dari Teorema C, perhatikan bahwa
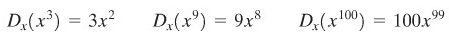
TEOREMA D: Aturan kelipatan konstanta
Jika \(k\) suatu konstanta dan \(f\) suatu fungsi yang terdiferensialkan, maka \((kf)'(x) = kf'(x)\); yakni

Bukti:
Andaikan \(F(x) = k.f(x)\). Maka

Contoh-contoh yang mengilustrasikan hasil-hasil ini adalah

TEOREMA E: Aturan jumlah
Jika \(f\) dan \(g\) fungsi-fungsi yang terdiferensialkan, maka \((f + g)'(x) = f'(x) + g'(x)\); yakni

Bukti:
Andaikan \(F(x) = f(x) + g(x)\). Maka

TEOREMA F: Aturan Selisih
Jika \(f\) dan \(g\) fungsi-fungsi yang terdiferensialkan, maka \((f - g)'(x) = f'(x) - g'(x)\); yakni

CONTOH 1:
Cari turunan dari \(5x^2 + 7x - 6\) dan \(4x^6 - 3x^5 - 10x^2 + 5x + 16\).
Penyelesaian:

Untuk mencari turunan berikutnya perhatikan bahwa teorema-teorema pada jumlah dan selisih meluas sampai sejumlah terhingga suku. Jadi,

Aturan Hasil Kali dan Hasil Bagi
Sekarang kita siap untuk suatu kejutan. Turunan hasil kali fungsi-fungsi tidak sama dengan hasilkali turunan fungsi-fungsi.
CONTOH 2:
Misalkan \(g(x) = x, h(x) = 1 + 2x,\) dan \(f(x) = g(x).h(x) = x(1 + 2x)\). Cari \(D_x f(x), D_x g(x), D_x h(x)\), dan tunjukkan bahwa \(D_x f(x) ≠ [D_x g(x)][D_x h(x)]\).
Penyelesaian:
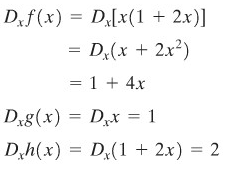
Perhatikan bahwa

di mana
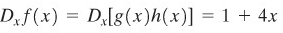
Dengan demikian, \(D_x f(x) ≠ [D_x g(x)][D_x h(x)]\).
TEOREMA G: Aturan Hasil Kali
Andaikan \(f\) dan \(g\) fungsi-fungsi yang dapat didiferensialkan, maka
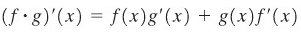
Yakni

Bukti:
Andaikan \(F(x) = f(x).g(x)\). Maka

CONTOH 3:
Gunakan Aturan hasilkali untuk mencari turunan \((3x^2- 5)(2x^4- x)\). Periksa jawaban dengan mengerjakan soal itu secara lain.
Penyelesaian:
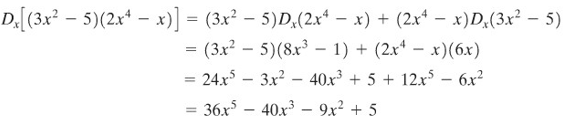
Untuk memeriksa, pertama kita kalikan dan kemudian ambil turunan.

Jadi,

TEOREMA H: Aturan Hasilbagi
Andaikan \(f\) dan \(g\) fungsi-fungsi yang dapat didiferensialkan dengan \(g(x) ≠ 0\). Maka

yakni

Bukti:
Andaikan \(F(x) = f(x)/g(x)\). Maka

CONTOH 4:
Cari turunan dari \((3x - 5)/(x^2 + 7)\)
Penyelesaian:

CONTOH 5:
Carilah turunan dari \(y = 2/(x^4+ 1) + 3/x\).
Penyelesaian:

Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Knowledge comes from learning. Wisdom comes from living.
