www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Integral › Definisi Integral Riemann
Definisi Integral Riemann
Pada artikel yang lalu, kita telah mempelajari integral tak tentu dan juga bagaimana mencari luas suatu daerah menggunakan poligon dalam dan poligon luar. Pada artikel ini kita akan mendefinisikan integral tentu. Kita mulai dengan mendefinisikan apa yang dimaksud dengan jumlah Riemann terlebih dahulu.
Jumlah Riemann
Pandang sebuah fungsi f yang didefinisikan pada selang tertutup [a,b]. Ia boleh bernilai positif ataupun negatif pada selang tersebut dan bahkan ia tidak perlu kontinu. Grafiknya mungkin seperti fungsi yang ada dalam Gambar 1.

Gambar 1
Selanjutnya, perhatikan suatu partisi \(P\) dari selang \([a,b]\) menjadi \(n\) selang bagian (tidak perlu berpanjang sama) memakai titik-titik
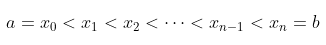
dan andaikan \(Δx_i=x_i-x_{i-1}\). Pada tiap selang bagian \([x_{i-1}, x_i ]\), ambil sebuah titik sebarang \(\overline{x}_i\) (yang mungkin saja sebuah titik ujung); kita sebut ia sebuah titik sampel untuk selang bagian ke-i. Sebuah contoh dari konstruksi ini diperlihatkan dalam Gambar 2 untuk \(n = 6\).

Gambar 2
Kemudian bentuklah penjumlahan sebagai berikut.

Kita sebut \(R_P\) sebagai jumlah Riemann untuk \(f\) yang berpadanan dengan partisi \(P\). Tafsiran geometrinya diperlihatkan pada Gambar 3.
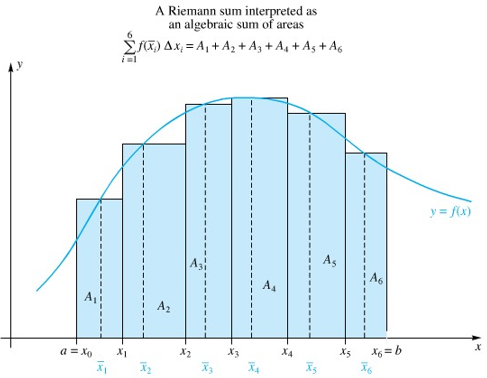
Gambar 3
CONTOH 1:
Hitung jumlah Riemann untuk \(f(x)=x^2+1\) pada interval \([-1,2]\) menggunakan titik-titik partisi yang sama panjang \(-1 < -0,5 < 0 < 0,5 < 1 < 1,5 < 2\), dengan titik sampel yang berpadanan \(\overline{x}_i\) adalah titik tengah dari subinterval ke-i.
Penyelesaian:
Gambar 4 di bawah memperlihatkan grafik untuk fungsi \(f(x)=x^2+1\) pada interval \([-1,2]\) beserta titik-titik partisi dan titik sampel yang dimaksud.

Gambar 4
Dengan demikian, diperoleh jumlah Riemann yaitu

Fungsi pada Gambar 3 dan 4 adalah positif. Akibatnya, jumlah Riemann hanyalah merupakan jumlah area persegi panjang (rectangles). Tetapi bagaimana jika f adalah negatif? Dalam kasus ini, suatu titik sampel \(\overline{x}_i\) dengan sifat bahwa \(f(\overline{x}_i)<0\) akan menyebabkan persegi panjang yang seluruhnya berada di bawah sumbu-x, dan perkalian \(f(x_i)Δx_i\) akan menjadi negatif.
Ini berarti bahwa kontribusi persegi panjang tersebut kepada jumlah Riemann adalah negatif. Gambar 5 mengilustrasikan ini.

Gambar 5
CONTOH 2:
Hitung jumlah Riemann \(R_P\) untuk
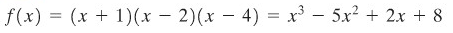
pada selang [0,5] memakai partisi \(P\) dengan titik-titik partisi \(0 < 1,1 < 2 < 3,2 < 4 < 5\) dan titik-titik sampel yang berpadanan \(\overline{x}_1 = 0,5; \overline{x}_2 = 1,5; \overline{x}_3=2,5; \overline{x}_4=3,6\) dan \(\overline{x}_5=5\).
Penyelesaian:
Gambar geometri yang berpadanan ditunjukkan pada Gambar 6.

Gambar 6
Dengan demikian, diperoleh jumlah Riemann yaitu

Definisi Integral Tentu
Sekarang andaikan bahwa \(P, Δx_i\), dan \(\overline{x}_i\) mempunyai arti seperti yang dibahas di atas. Tetapkan juga \(|P|\), disebut norma \(P\), yang menyatakan panjang selang bagian yang terpanjang dari partisi \(P\). Misalnya, pada contoh 1, \(|P|=3,2-2=1,2\); pada Contoh 2, \(|P|=0,5\).
DEFINISI: Integral Tentu
Andaikan \(f\) suatu fungsi yang didefinisikan pada selang tertutup \([a,b]\). Jika

ada, kita katakan \(f\) adalah terintegralkan pada \([a,b]\). Lebih lanjut, \(∫_a^b f(x) \ dx\), disebut integral tentu (atau integral Riemann) \(f\) dari \(a\) ke \(b\), diberikan oleh

Secara umum, \(∫_a^b f(x) \ dx\) menyatakan batasan luas daerah yang tercakup di antara kurva \(y=f(x)\) dan sumbu-x dalam selang \([a,b]\), yang berarti bahwa tanda positif akan diberikan pada luas bagian-bagian yang berada di bagian atas sumbu-x dan tanda negatif diberikan untuk luas bagian-bagian yang berada di bawah sumbu-x. Secara simbolik,

di mana \(A_{up}\) dan \(A_{down}\) adalah seperti diperlihatkan dalam Gambar 7.

Gambar 7
Kembali ke lambang \(∫_a^b f(x) dx\), kita boleh menyebut \(a\) titik ujung bawah dan \(b\) titik ujung atas untuk integral. Tetapi, kebanyakan pengarang memakai istilah batas bawah pengintegralan dan batas atas pengintegralan, yang adalah baik asal saja disadari bahwa pemakaian kata batas tidak dikacaukan dengan artinya yang lebih teknis.
Dalam definisi \(∫_a^b f(x) \ dx\), kita, secara implisit menganggap bahwa \(a < b\). Kita hilangkan batasan itu dengan definisi-definisi berikut.
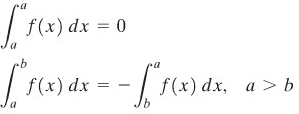
Jadi, kita dapat tuliskan

Akhirnya, kita tunjukkan bahwa \(x\) adalah variabel dummy dalam lambang \(∫_a^b f(x) \ dx\). Dengan ini kita maksudkan bahwa \(x\) dapat diganti oleh huruf sebarang lain (tentu saja, asal ia diganti di setiap tempat kemunculannya). Jadi,

Fungsi-fungsi apa yang dapat diintegralkan?
Tidak setiap fungsi dapat diintegralkan pada selang tertutup \([a,b]\). Misalnya, fungsi yang tak terbatas
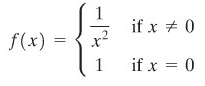
yang digrafikkan pada Gambar 8, tak terintegralkan pada \([-2,2]\). Karena kontribusi kepada sebarang jumlah Riemann dari selang bagian yang mengandung \(x = 0\) dapat dibuat berapa pun besarnya dengan cara pemilihan titik sampel \(\overline{x}_i\) yang berpadanan cukup dekat ke nol.
Penalaran ini menunjukkan bahwa sebarang fungsi yang terintegralkan pada \([a,b]\) harus terbatas di sana; yakni, harus terdapat konstanta M sedemikian sehingga \(|f(x)|≤M\) untuk semua \(x\) dalam \([a,b]\).
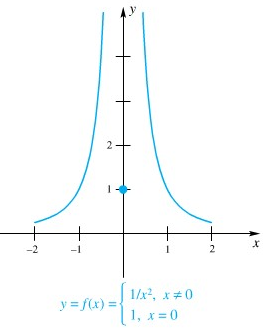
Gambar 8
TEOREMA:
Jika \(f\) terbatas pada \([a,b]\) dan ia kontinu di sana kecuali pada sejumlah terhingga titik, maka \(f\) terintegralkan pada \([a,b]\). Khususnya, jika \(f\) kontinu pada seluruh selang \([a,b]\), maka ia terintegralkan pada \([a,b]\).
Sebagai konsekuensi dari teorema ini, fungsi-fungsi berikut adalah terintegralkan pada setiap selang tertutup [a,b].
1. Fungsi-fungsi polinom
2. Fungsi-fungsi sinus dan kosinus
3. Fungsi-fungsi rasional, asalkan [a,b] tidak mengandung titik-titk yang mengakibatkan suatu penyebut 0.
Penghitungan Integral Tentu
Dengan mengetahui bahwa suatu fungsi adalah terintegralkan, maka kita boleh menghitung integralnya memakai suatu partisi tetap (selang bagian sama panjang) dan dengan mengambil titik sampel \(x_i\) dalam cara yang mudah untuk kita. Contoh 3 dan 4 meliputi polinom, yang baru saja kita pelajari adalah terintegralkan.
CONTOH 3:

Penyelesaian:
Partisikan selang \([-2,3]\) menjadi \(n\) selang bagian yang sama, masing-masing dengan panjang \(Δx=5/n\). Dalam tiap selang bagian \([x_{i-1}, x_i]\) gunakan \(\overline{x}_i=x_i\) sebagai titik sampel. Maka,

Dengan demikian, \(f(x_i)=x_i+3=1+i \left(\frac{5}{n}\right)\), dan sehingga

Karena \(P\) adalah suatu partisi tetap, \(|P|→0\) setara dengan \(n→∞\). Kita simpulkan bahwa

Jawaban kita pada Contoh 3 ini tidaklah mengherankan karena integral yang akan kita cari tak lain adalah suatu trapesium yang diperlihatkan pada Gambar 9. Kita dapat juga menghitungnya memakai rumus di sekolah menengah, tetapi untuk mahasiswa lebih menarik mengerjakannya secara lebih rumit.

Gambar 9
CONTOH 4:
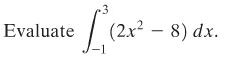
Penyelesaian:
Gambar 10 menunjukkan grafik fungsi yang dimaksud dengan \(A_1\) dan \(A_2\) adalah luas-luas daerah di bawah dan di atas sumbu x.

Gambar 10
Andaikan \(P\) suatu partisi tetap dari \([-1,3]\) atas \(n\) selang bagian sama, masing-masing sepanjang \(Δx=4/n\). Dalam tiap selang bagian \([x_{i-1}, x_i]\), pilih \(\overline{x}_i\) berupa titik ujung kanan, sehingga \(\overline{x}_i=x_i\). Maka
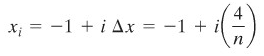
dan

Akibatnya,
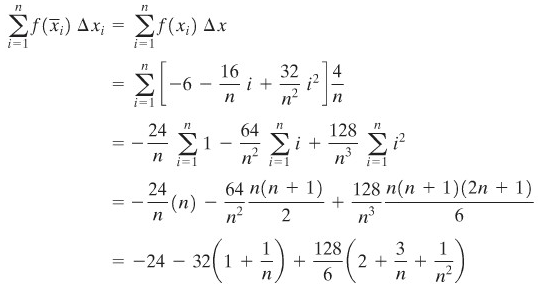
Kita simpulkan bahwa

Bahwa jawaban adalah negatif tidak mengherankan, karena daerah di bawah sumbu-x lebih luas dari pada yang di atas sumbu-x (Gambar 10).
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Bermimpilah dalam hidup, jangan hidup dalam mimpi.
