Contoh 1:

Hitung nilai limit berikut: \( \displaystyle{ \lim_{x\to 1} \frac{x^3-1}{\sqrt{2x+2}-2} } \)

Pembahasan:

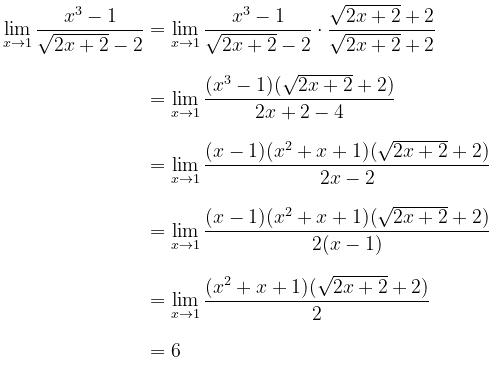
Contoh 2:

Tentukan nilai \(a\) yang memenuhi persamaan berikut:

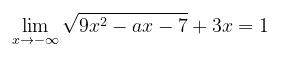
Pembahasan:

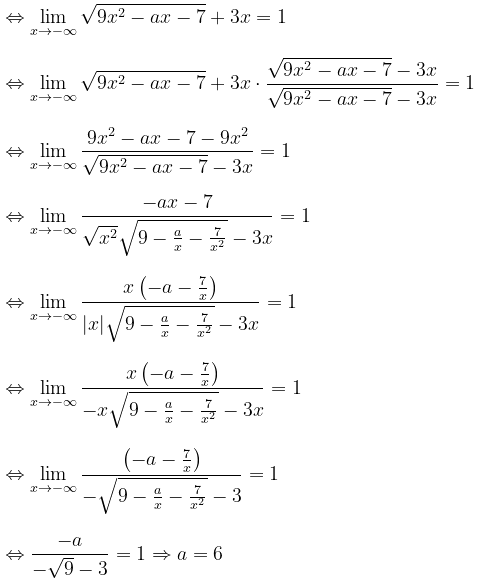
Jadi, nilai \(a\) yang memenuhi adalah 6.

Contoh 3:

Tentukan nilai \(a\) yang memenuhi persamaan berikut:

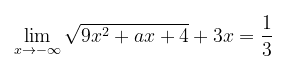
Pembahasan:

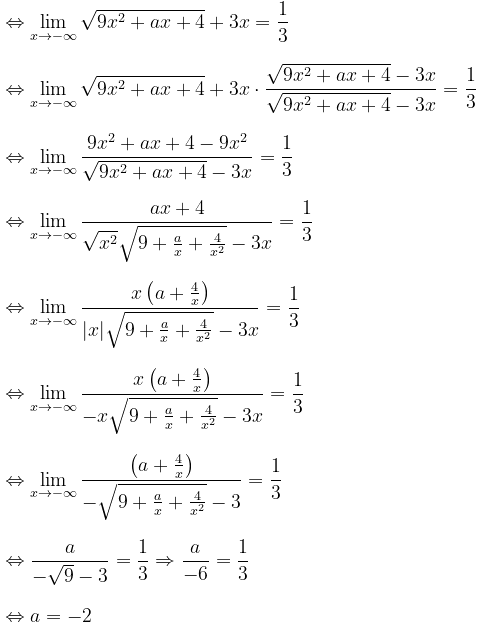
Jadi, nilai \(a\) yang memenuhi adalah -2.

Contoh 4:

Tentukan nilai \(a\) agar fungsi

mempunyai limit di \(x = 0\).

Pembahasan:

Agar \(f(x)\) memiliki limit di \(x = 0\) maka haruslah limit kiri dan limit kanannya sama, yakni

\[ \lim_{x\to 0^-} f(x) = \lim_{x\to 0^+} f(x) \]

di mana limit kirinya, yaitu:

\[ \lim_{x\to 0^-} f(x) = \lim_{x\to 0^-} \frac{\sin{ax}}{x} = a \]

dan limit kanannya, yaitu:

\[ \lim_{x\to 0^+} f(x) = \lim_{x\to 0^+} x + 1 = 1 \]

Dengan demikian, \(a\) harus bernilai 1 agar \(f(x)\) memiliki limit di \(x = 0\).

Contoh 5:

Tentukan \(a\) dan \(b\) sehingga

\[ \displaystyle{ \lim_{x\to 0} \frac{a+\cos{(bx)}}{x^2} = -2} \]

Pembahasan:

Pertama, \(\displaystyle{ \lim_{x\to 0} a+\cos{(bx)} } \) haruslah bernilai 0. Sebab jika hal ini tidak terjadi (katakanlah \(\displaystyle{ \lim_{x\to 0} a+\cos{(bx)} = c \neq 0 } \) ) akan berakibat

\[ \lim_{x\to 0} \frac{a+\cos{(bx)}}{x^2} = \frac{c}{ \displaystyle \lim_{x\to 0} x^2} = \infty \]

yang bertentangan dengan pernyataan

\[ \lim_{x\to 0} \frac{a+\cos{(bx)}}{x^2} = -2 \]

Dengan demikian, kita peroleh

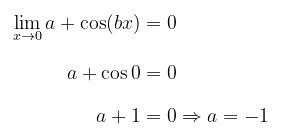
Kemudian karena \(\displaystyle{ \lim_{x\to 0} \frac{a+\cos{(bx)}}{x^2} } \) berbentuk \( \frac{0}{0} \) untuk \(a = -1\), maka kita dapat menerapkan dalil I’Hopital yakni

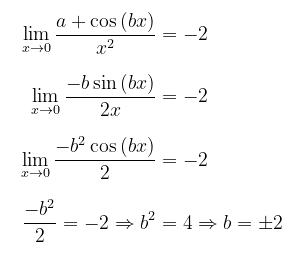
Jadi, nilai \(b\) adalah \(±2\).