www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS I
Kalkulus I
Kalkulus 1 › Integral Tak wajar › Contoh soal dan pembahasan Integral Tak Wajar
Integral Tak wajar
Contoh soal dan pembahasan Integral Tak Wajar
Contoh 1:
Selesaikanlah integral \( \displaystyle \int_{-1}^{+\infty} \frac{x}{1 + x^2} \ dx \).
Pembahasan:
Pertama, hitung integral dengan mengabaikan batas pengintegralannya terlebih dahulu. Kita bisa selesaikan integral ini dengan teknik substitusi. Dengan memisalkan \( u = x^2\), kita peroleh berikut ini:
\begin{aligned} \frac{du}{dx} = 2x \Leftrightarrow dx = \frac{du}{2x} \end{aligned}
Sehingga,
Dengan demikian,
Contoh 2:
Selesaikanlah integral 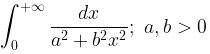
Pembahasan:
Pertama, kita hitung integral dengan mengabaikan batas pengintegralannya terlebih dahulu. Kita bisa selesaikan integral ini dengan teknik substitusi. Dengan memisalkan: \( u = bx \), maka
\[ \frac{du}{dx} = b \Leftrightarrow dx = \frac{du}{b} \]
Sehingga
Dengan demikian,
Contoh 3:
Selesaikanlah integral \( \displaystyle \int_{0}^{4} \frac{dx}{(x-2)^{2/3}} \).
Pembahasan:
Soal ini merupakan contoh integral tak wajar dengan integran yang tak-terhingga pada sebuah titik dalam (ada nilai di antara 0 dan 4 yang membuat fungsi tersebut tak-terhingga). Perhatikan bahwa integran ini tak terhingga pada \(x = 2\). Untuk menyelesaian integral demikian, kita bisa membaginya menjadi dua yakni:
Selanjutnya, kita hitung integral dengan mengabaikan batas pengintegralannya terlebih dahulu. Hasil dari pengintegralannya, yaitu:
\begin{aligned} \int \frac{1}{(x-2)^{2/3}} \ dx = 3(x-2)^{1/3} + C \end{aligned}
Dengan demikian, kita peroleh berikut ini:
Contoh 4:
Selesaikanlah integral \( \displaystyle \int_{e}^{\infty} \frac{1}{x \ln^3 x} \ dx \).
Pembahasan:
Hitung integral dengan mengabaikan batas pengintegralannya terlebih dahulu. Kita bisa selesaikan integral ini dengan teknik substitusi. Misalkan \(u = \ln x\) sehingga \( du = 1/x \ dx\). Selanjutnya, kita peroleh berikut.
Dengan demikian, kita dapatkan hasil berikut:
Contoh 5:
Selesaikanlah integral \( \displaystyle \int_{-\infty}^{+\infty} \frac{e^{-x}}{1 + e^{-2x}} \ dt \).
Pembahasan:
Hitung integral dengan mengabaikan batas pengintegralannya terlebih dahulu. Kita bisa selesaikan integral ini dengan teknik substitusi. Dengan memisalkan \(u = e^{-x}\), maka
\[ \frac{du}{dx} = -e^{-x} \Leftrightarrow dx = \frac{du}{-e^{-x}} = \frac{du}{-u} \]
Selanjutnya, dari hasil di atas, kita peroleh berikut ini:
Dengan demikian, kita dapatkan hasil berikut:
Contoh 6:
Tentukan nilai \(a\) yang memenuhi \( \displaystyle \int_{0}^{+\infty} e^{-ax} \ dx = 5 \).
Pembahasan:
\begin{aligned} \int_{0}^{+\infty} e^{-ax} \ dx = 5 &\Leftrightarrow \lim_{b\to +\infty} \int_{0}^{b} e^{-ax} \ dx = 5 \\[8pt] &\Leftrightarrow \lim_{b\to +\infty} \left[ -\frac{1}{a} e^{-ax} \right]_0^b = 5 \\[8pt] &\Leftrightarrow \lim_{b\to +\infty} \left[ -\frac{1}{a} e^{-ab} + \frac{1}{a} e^{-a(0)} \right] = 5 \\[8pt] &\Leftrightarrow -\frac{1}{a} e^{-a(+\infty)} + \frac{1}{a} e^0 = 5 \\[8pt] &\Leftrightarrow 0 + \frac{1}{a} = 5 \\[8pt] &\Leftrightarrow a = \frac{1}{5} \end{aligned}
Contoh 7:
Tentukan nilai \(a\) yang memenuhi \( \displaystyle \int_{0}^{+\infty} \frac{1}{x^2 + a^2} \ dx = 1, \ a > 0 \).
Pembahasan:
\begin{aligned} \int_{0}^{+\infty} \frac{1}{x^2 + a^2} \ dx = 1 &\Leftrightarrow \lim_{b\to +\infty} \int_{0}^{b} \left[ \frac{1}{a} \tan^{-1} \frac{x}{a} \right]_0^b = 1 \\[8pt] &\Leftrightarrow \lim_{b\to +\infty} \left[ \frac{1}{a} \tan^{-1} \frac{b}{a} - \frac{1}{a} \tan^{-1} 0 \right] = 1 \\[8pt] &\Leftrightarrow \frac{1}{a} \tan^{-1} \frac{+\infty}{a} - \frac{1}{a} (0) = 1 \\[8pt] &\Leftrightarrow \frac{1}{a} \tan^{-1} \infty = 1 \\[8pt] &\Leftrightarrow \frac{1}{a} \frac{\pi}{2} = 1 \\[8pt] &\Leftrightarrow a = \frac{\pi}{2} \end{aligned}
Contoh 8:
Tentukan kekonvergenan integral 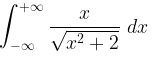
Pembahasan:
Hitung integral dengan mengabaikan batas pengintegralannya terlebih dahulu. Misalkan \(\tan \theta = x/\sqrt{2}\), maka
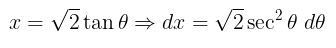
Ingat bahwa karena tadi kita memisalkan \( \tan \theta = x/\sqrt{2} \), maka \( \sec \theta = \sqrt{x^2+2}{\sqrt{2}} \). Perhatikan gambar berikut.
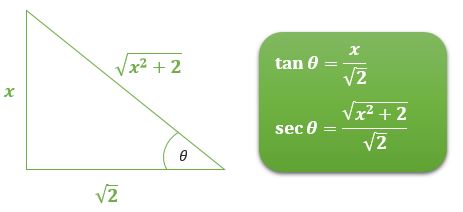
Selanjutnya, kerjakan pengintegralan berikut.
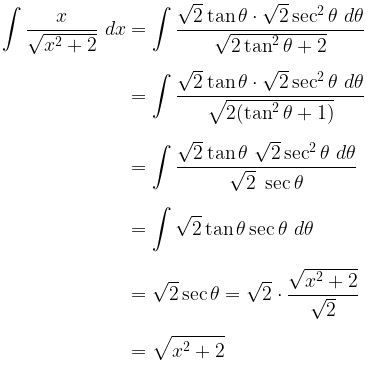
Dengan demikian,
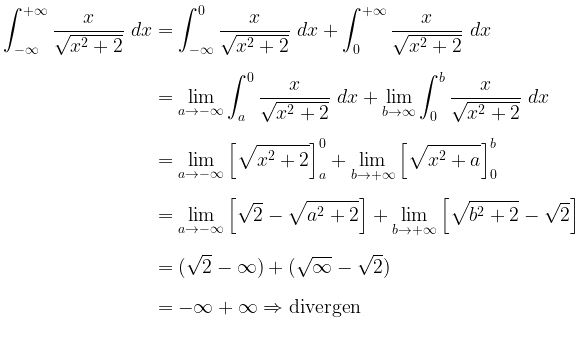
Dalam integral tak wajar, jika nilai integralnya ada maka dikatakan integral tersebut konvergen, dan jika tidak ada, maka dikatakan divergen. Dalam hasil di atas, nilai integralnya tidak ada sehingga dikatakan divergen.
Contoh 9:
Selesaikanlah integral 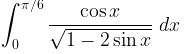
Pembahasan:
Hitung integral dengan mengabaikan batas pengintegralannya terlebih dahulu. Misalkan \( u = \sin x\), maka
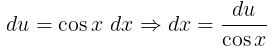
Selanjutnya, kita peroleh berikut:
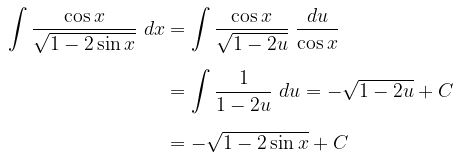
Dengan demikian,

Contoh 10:
Selesaikanlah integral 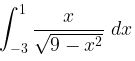
Pembahasan:
Hitung integral dengan mengabaikan batas pengintegralannya terlebih dahulu. Misalkan \( x = 3 \sin \theta \), maka \( dx = 3 \cos \theta \ d\theta \). Perhatikan gambar berikut.
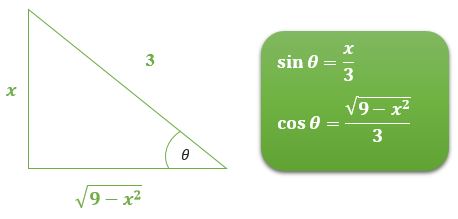
Selanjutnya, kita peroleh:
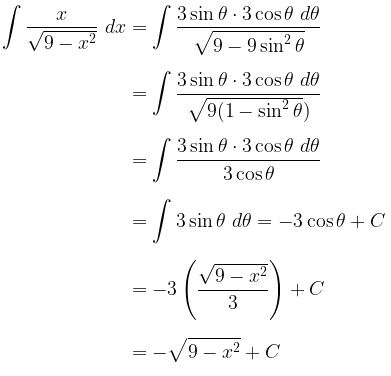
Dengan demikian,
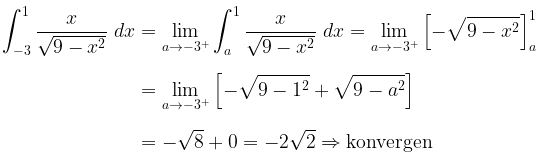
Contoh 11:
Tentukanlah \( \displaystyle \int_{0}^{+\infty} \frac{e^{-x}}{\sqrt{x}} \ dx \) jika diketahui \( \displaystyle \int_{0}^{+\infty} e^{-x^2} \ dx = \frac{1}{2} \sqrt{\pi} \).
Pembahasan:
Perhatikan bahwa
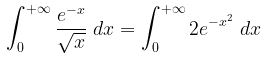
Untuk pembuktiannya kita bisa misalkan \( u = x^2 \to x = \sqrt{u} \), sehingga kita peroleh berikut ini:
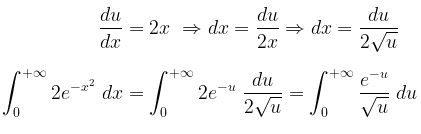
Dari hasil di atas, jika kita mengganti variabel pengintegralan \(u\) dengan \(x\), maka diperoleh integral seperti pada soal.
Dengan demikian, integral pada soal di atas dapat dikerjakan sebagai berikut:
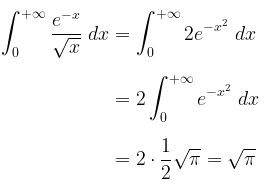
Contoh 12:
Tentukanlah \( \displaystyle \int_{0}^{+\infty} e^{-a^2x^2} \ dx, \ a > 0 \ \) jika diketahui \( \displaystyle \int_{0}^{+\infty} e^{-x^2} \ dx = \frac{1}{2} \sqrt{\pi} \).
Pembahasan:
Perhatikan bahwa
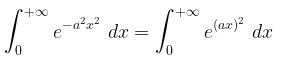
Misalkan \(u = ax\), maka kita peroleh:
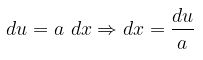
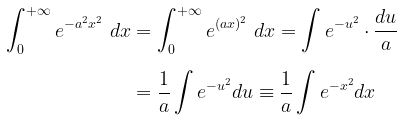
Dengan demikian,
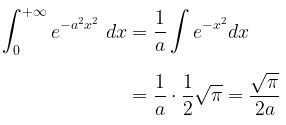
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
