Kalkulus 1 › Integral dengan Fungsi Gamma dan Fungsi Beta › Latihan soal dan pembahasan Integral dengan Fungsi Gamma dan Fungsi Beta Bagian 2

Fungsi Gamma dan Fungsi Beta

Latihan soal dan pembahasan Integral dengan Fungsi Gamma dan Fungsi Beta Bagian 2

Guna memperdalam pemahaman tentang integral dengan fungsi gamma dan fungsi beta, berikut ini diberikan sejumlah latihan soal terkait materi tersebut beserta pembahasannya.

Soal Nomor 1

Hitunglah integral berikut:

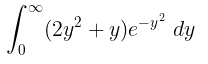
Pembahasan:

Ini merupakan contoh soal penyelesaian integral dengan fungsi gamma. Untuk menyelesaikan integral ini, misalkan \( m = y^2 \), maka \( y = \sqrt{m} \) dan \( dy = \frac{1}{2\sqrt{m}} \ dm \). Kemudian ubahlah batas pengintegralan di mana ketika \( y = 0 \to m = 0 \) dan \( y = \infty \to m = ∞ \). Dengan demikian, kita peroleh

Soal Nomor 2

Gunakan fungsi Beta untuk menyelesaikan .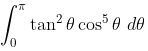

Pembahasan:

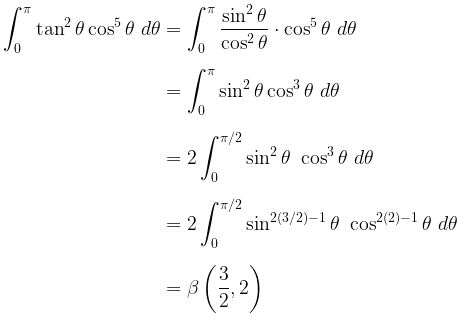
Selanjutnya, kita cari nilai dari \( \beta \left( \frac{3}{2}, 2 \right) \), yakni

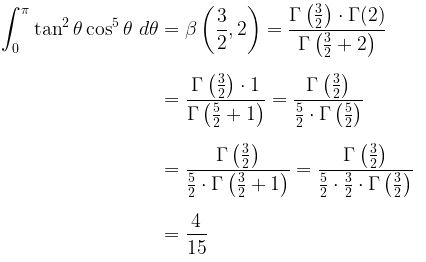
Soal Nomor 3

Dengan transformasi ke fungsi gamma, buktikan:

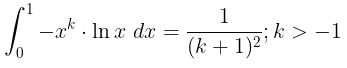
Pembahasan:

Misalkan y = - ln x, maka \( x = e^{-y} \) dan

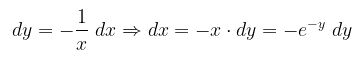
Kemudian ubah batas pengintegralan, yaitu:

Dengan demikian,

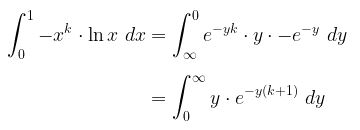
Catatan: Negatif hilang karena kita menukar batas atas dengan batas bawah pengintegralan.

Untuk menyelesaikan integral di atas, kita misalkan lagi: u = y (k + 1) sehingga

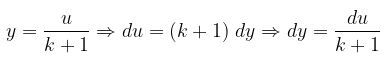
Kemudian ubah batas pengintegralan, yaitu:

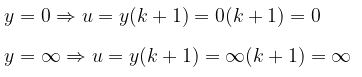
Selanjutnya, integral tersebut dapat dituliskan menjadi:

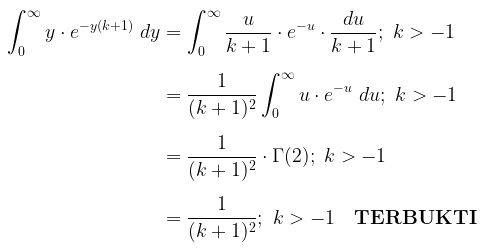
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.