www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Teori Peluang » Distribusi Peubah Acak Kontinu › Distribusi Lognormal
Peubah Acak Kontinu
Distribusi Lognormal
Distribusi lognormal digunakan untuk berbagai macam aplikasi. Distribusi berlaku jika transformasi log natural menghasilkan distribusi normal.
Distribusi lognormal digunakan untuk berbagai macam aplikasi. Distribusi berlaku jika transformasi log natural menghasilkan distribusi normal.
Definisi: PDF Distribusi Lognormal
Suatu peubah acak kontinu X akan mempunyai distribusi lognormal jika peubah acak Y = ln(X) mempunyai distribusi normal dengan rataan μ dan standar deviasi σ dengan fungsi kepadatan peluangnya (pdf) diberikan oleh
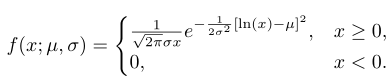
Adapun grafik dari distribusi lognormal diilustrasikan pada Gambar 1 berikut.
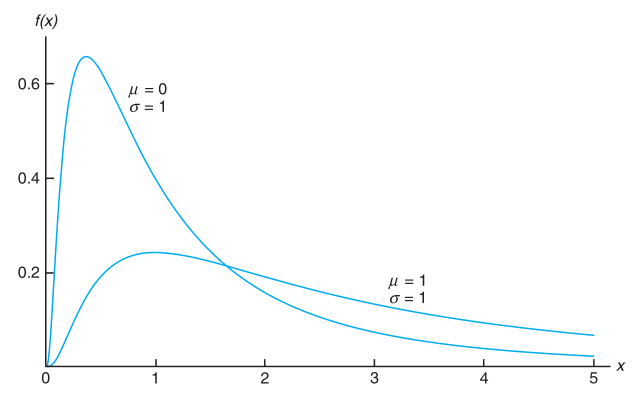
Gambar 1. Distribusi Lognormal
Rataan dan varians distribusi lognormal diberikan oleh rumus berikut.

Contoh 1:
Konsentrasi polutan yang dihasilkan oleh pabrik kimia secara historis diketahui menunjukkan perilaku yang menyerupai distribusi lognormal. Ini penting ketika seseorang mempertimbangkan masalah tentang kepatuhan (compliance) terhadap peraturan pemerintah. Misalkan diasumsikan bahwa konsentrasi polutan tertentu, dalam bagian per juta, memiliki distribusi lognormal dengan parameter μ = 3.2 dan σ = 1. Berapakah probabilitas bahwa konsentrasi melebihi 8 bagian per juta?
Pembahasan:
Misalkan X adalah konsentrasi polutan, maka
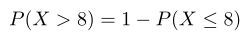
Karena ln(X) mempunyai distribusi normal dengan rataan μ = 3.2 and standar deviasi σ = 1, maka
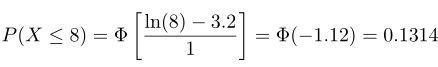
Di sini kita menggunakan Φ untuk menyatakan fungsi distribusi kumulatif dari distribusi normal standar. Akibatnya, probabilitas bahwa konsentrasi polutan melebihi 8 bagian per juta adalah 0.1314.
Contoh 2:
Lama hidup, dalam ribuan mil, jenis kontrol elektronik tertentu untuk lokomotif mempunyai distribusi yang mendekati distribusi lognormal dengan μ = 5.149 and σ = 0.737. Carilah persentil ke-5 dari masa pakai elektronik tersebut.
Pembahasan:
Dari tabel distribusi normal, kita tahu bahwa P(Z < -1,645) = 0.05. Lama hidup (umur) kontrol elektronik dilambangkan dengan X. Karena ln(X) mempunyai distribusi normal dengan μ = 5.149 and σ = 0.737, persentil ke-5 dapat dihitung sebagai berikut.
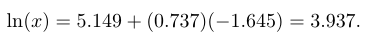
Jadi, x = 51.265. Ini berarti bahwa hanya 5% dari kontrol elektronik yang mempunyai lama hidup kurang dari 51,264 miles.
Sumber:
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
Artikel Terkait
Kindness is a language that the deaf can hear and the blind can see.
