www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Uji Kekonvergenan Deret Tak Hingga
Deret Pangkat, Deret Taylor, dan Deret Mac Laurin
Fungsi-Fungsi Peubah Banyak
Limit dan Kekontinuan Peubah Banyak
Turunan Fungsi Peubah Banyak
Integral Lipat Dua
Integral Lipat Tiga
Transformasi Koordinat dalam Integral Lipat
Kalkulus II » Turunan Fungsi Peubah Banyak › Turunan Fungsi Implisit untuk Beberapa Variabel - Materi, Contoh Soal dan Pembahasan
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Turunan
Turunan Fungsi Implisit untuk Beberapa Variabel - Materi, Contoh Soal dan Pembahasan
Kita telah membahas cara mencari turunan fungsi implisit untuk dua variabel atau dua peubah dalam materi kalkulus I yang disajikan di website ini. Pada artikel ini, kita akan lanjutkan pembahasan tersebut untuk mencari turunan fungsi implisit untuk beberapa variabel.
Misalkan terdapat fungsi \( F(x,y)=0 \) di mana \(y\) adalah fungsi implisit dari \(x\). Untuk mencari turunan dari fungsi implisit \(y\) atau \( \displaystyle \frac{dy}{dx} \), kita dapat menggunakan aturan rantai. Bagi Anda yang belum paham mengenai aturan rantai, Anda dapat membaca materinya terlebih dahulu di artikel ini: Aturan Rantai untuk mencari turunan fungsi beberapa variabel.
Jika kita turunkan kedua ruas \(F(x,y)=0\) terhadap \(x\) dengan menggunakan Aturan Rantai. Kita peroleh
\begin{aligned} \frac{\partial F}{\partial x} \cdot \frac{dx}{dx} + \frac{\partial F}{\partial y} \cdot \frac{dy}{dx} &= 0 \\[8pt] \frac{\partial F}{\partial x} + \frac{\partial F}{\partial y} \cdot \frac{dy}{dx} &= 0 \\[8pt] \frac{\partial F}{\partial y} \cdot \frac{dy}{dx} &= - \frac{\partial F}{\partial x} \\[8pt] \frac{dy}{dx} &= - \frac{ \frac{\partial F}{\partial x} }{ \frac{\partial F}{\partial y} } \\[8pt] \frac{dy}{dx} &= - \frac{F_x(x,y)}{F_y(x,y)} \end{aligned}
Contoh 1:
Carilah \( \displaystyle \frac{dy}{dx} \) jika diketahui \(x^3+x^2 y-10y^4=0\) menggunakan (a) Aturan rantai dan (b) Turunan implisit.
Pembahasan:
(a). Metode Aturan Rantai. Andaikan \(F(x,y)=x^3+x^2 y-10y^4\), maka sesuai rumus aturan rantai, diperoleh:
\begin{aligned} \frac{dy}{dx} &= - \frac{ \partial F/ \partial x}{ \partial F/ \partial y } \\[8pt] \frac{dy}{dx} &= - \frac{3x^2+2xy}{x^2-40y^3} \end{aligned}
(b). Metode Turunan Implisit. Berdasarkan metode ini, turunkan kedua sisi persamaan \(F(x,y)\) terhadap \(x\) sehingga diperoleh:
\begin{aligned} 3x^2+x^2 \ \frac{dy}{dx}+ 2xy-40y^3 \ \frac{dy}{dx} &= 0 \\[8pt] (x^2-40y^3) \ \frac{dy}{dx} &= -(3x^2+2xy) \\[8pt] \frac{dy}{dx} &= - \frac{3x^2+2xy}{x^2-40y^3} \end{aligned}
Perhatikan bahwa kedua metode tersebut menghasilkan jawaban yang sama.
Contoh di atas merupakan kasus untuk dua variabel. Sekarang kita akan beralih ke kasus tiga variabel. Cara pengerjaannya masih sama. Jika \(z\) suatu fungsi implisit dari \(x\) dan \(y\) yang didefinisikan oleh persamaan \(F(x,y,z)=0\), maka penurunan kedua ruas terhadap \(x\) dengan mempertahankan \(y\) tetap menghasilkan
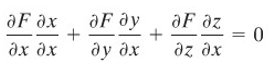
Dari hasil di atas, jika kita selesaikan untuk \(∂z/∂x\) dan dengan mencatat bahwa \(∂y/∂x=0\), kita peroleh rumus pertama di bawah. Perhitungan yang serupa dengan mempertahankan \(x\) tetap dan menurunkan terhadap \(y\) menghasilkan rumus yang kedua.
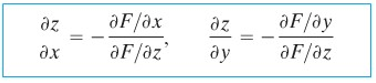
Contoh 2:
Jika \(F(x,y,z)=x^3 e^{y+z}-y \sin{(x-z)}=0\) mendefinisikan \(z\) secara implisit sebagai suatu fungsi \(x\) dan \(y\), tentukan \(∂z/∂x\).
Pembahasan:
Kita bisa selesaikan soal turunan implisit ini menggunakan rumus aturan rantai seperti yang diberikan di atas.
\begin{aligned} \frac{\partial z}{\partial x } &= -\frac{\partial F / \partial x}{ \partial F / \partial z } \\[8pt] &= -\frac{3x^2 e^{y+z}-y \cos(x-z)}{x^3 e^{y+z}+y \cos(x-z)} \end{aligned}
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
Service to others is the rent you pay for your room here on earth.
Muhammad Ali