Kalkulus II   »   Integral Lipat Dua   ›  Luas Daerah dengan Menggunakan Integral Lipat Dua - Materi, Contoh Soal dan Pembahasan

Integral Lipat

Luas Daerah dengan Menggunakan Integral Lipat Dua - Materi, Contoh Soal dan Pembahasan

Anggaplah bahwa \(G\) adalah sebuah permukaan di atas daerah tertutup dan terbatas \(S\) pada bidang \(xy\). Asumsikan bahwa \(f\) kontinu pada turunan parsial pertama \(f_x\) dan \(f_y\). Kita mulai dengan membentuk suatu partisi \(P\) terhadap daerah \(S\) dengan garis-garis yang sejajar sumbu \(x\) dan \(y\) (lihat Gambar 1).

Misalkan \(R_m, \ m=1,2,…,n\) menunjukkan persegi panjang yang sepenuhnya terletak di dalam \(S\). Untuk setiap \(m\), misalkan \(G_m\) merupakan bagian dari permukaan \(G\) yang diproyeksikan terhadap \(R_m\) dan misalkan \(P_m\) adalah titik pada \(G_m\) yang diproyeksikan terhadap pojok \(R_m\) dengan koordinat \(x\) dan \(y\) yang paling kecil. Akhirnya, andaikan \(T_m\) menyatakan jajaran genjang dari bidang singgung pada Pm yang diproyeksikan terhadap \(R_m\), seperti ditunjukkan pada Gambar 1, dan lebih rincinya pada Gambar 2.

Gambar 1 (Kiri) dan 2 (Kanan)

Selanjutnya, kita mencari luas jajar genjang \(Tm\) yang mana proyeksinya adalah \(Rm\). Misalkan \(u_m\) dan \(v_m\) menyatakan vektor yang membentuk sisi \(Tm\), maka

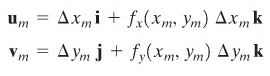
Dari pelajaran kita sebelumnya, kita tahu bahwa luas jajar genjang \(Tm\) adalah \(‖u_m×v_m‖\), di mana

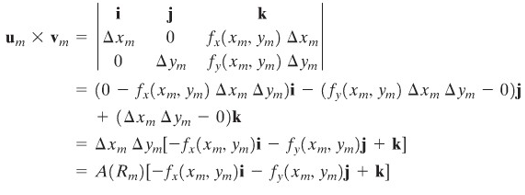
Sehingga, luas \(Tm\) adalah

Kemudian kita menambahkan luas jajar genjang singgung tersebut \(Tm, \ m = 1, 2, …, n\) dan mengambil limit untuk mendapatkan luas permukaan \(G\). Jika norma \(|P|\) partisi S adalah kecil, maka himpunan jajaran genjang singgung \(Tm\) akan mengaproksimasi permukaan \(G\), dan semakin kecil \(|P|\) dibuat, makin baik aproksimasi tersebut. Luas permukaan \(G\) didefinisikan sebagai

atau lebih tepatnya,

Gambar 1 digambarkan seakan-akan daerah \(S\) dalam bidang \(xy\) adalah persegi panjang; sering kali daerah \(S\) tidak berbentuk persegi panjang. Gambar 3 menunjukkan apa yang terjadi ketika \(S\) bukan sebuah persegi panjang.

Gambar 3

Sumber:

Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Penerbit Erlangga.

Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.