Kalkulus II   »   Fungsi Peubah banyak   ›  Pengertian Fungsi Peubah Banyak

Fungsi

Pengertian Fungsi Peubah Banyak

Fungsi \(f\) merupakan fungsi dua peubah jika \(f\) memetakan pasangan dua buah bilangan real \((x,y)\) ke suatu bilangan real \(f(x,y)\).

---

Fungsi \(f\) merupakan fungsi dua peubah jika \(f\) memetakan pasangan dua buah bilangan real \((x,y)∈D_f⊆R^2\) ke suatu bilangan real \(f(x,y)\).

Himpunan \(D_f\) disebut dengan domain atau daerah asal fungsi dan himpunan semua nilai \(f(x,y)\), dengan \((x,y)∈D_f\) disebut dengan daerah hasil (range) \(f\), dan dinotasikan dengan \(R_f\) (Gambar 1). Jika daerah asal fungsi tidak diperinci, kita ambil D berupa daerah asal mulanya (natural domain), yakni himpunan semua titik \((x,y)\) pada bidang di mana aturan fungsi berlaku dan menghasilkan suatu bilangan riil.

Misal, untuk \(f(x,y)=x^2+3y^2\), daerah mulanya adalah seluruh bidang; untuk \(g(x,y)=2x \sqrt{y}\), daerah asal mulanya adalah \(\{(x,y):x∈R,y≥0\}\).

Gambar 1.

Dengan demikian,

dan

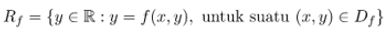
Semua yang telah dijelaskan di atas dapat meluas menjadi fungsi dari tiga peubah rill atau bahkan n peubah riil.

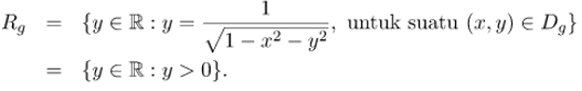
Sumber:

Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Penerbit Erlangga.

Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.