www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Uji Kekonvergenan Deret Tak Hingga › Uji Integral - Materi, Contoh Soal dan Pembahasan
Deret
Uji Integral - Materi, Contoh Soal dan Pembahasan
Sesuai namanya, uji integral menggunakan konsep integral atau lebih tepatnya integral tak wajar (karena batas atas integral berupa nilai tak hingga) untuk menentukan kekonvergenan deret.
Uji kekonvergenan deret tak hingga yang lain dikenal dengan uji integral. Sesuai dengan namanya, uji ini menggunakan konsep integral atau lebih tepatnya integral tak wajar (karena batas atas integral berupa nilai tak hingga) untuk menentukan kekonvergenan deret. Kita nyatakan uji ini dalam teorema berikut.
Teorema: Uji Integral
Andaikan \(f\) adalah fungsi yang kontinu, positif dan turun pada selang \([k, ∞]\). Andaikan \(f(n) = a_n\) untuk semua \(n\) positif bulat.
- Jika \( \int_k^\infty f(x) \ dx \) adalah konvergen maka \( \displaystyle{\sum_{n=k}^\infty} a_n \) juga konvergen.
- Jika \( \int_k^\infty f(x) \ dx \) adalah divergen maka \( \displaystyle{\sum_{n=k}^\infty} a_n \) juga divergen.
Terdapat bebarapa hal yang perlu dicatat terkait uji integral ini. Pertama, batas bawah pada integral tak wajar (improper integral) harus mempunyai nilai yang sama dengan nilai awal yang memulai deret tersebut. Dengan kata lain, jika deret dimulai dengan n = 1, maka batas bawah integral juga harus sama dengan 1.
Kedua, fungsi tidak harus selalu turun dan positif di mana-mana pada interval yang diberikan sesuai dengan teorema di atas. Yang penting adalah fungsi tersebut pada akhirnya akan turun dan positif. Dengan kata lain, tidaklah masalah jika fungsinya naik atau negatif untuk sesaat pada selang interval tertentu, tapi yang penting pada akhirnya fungsi harus turun dan positif.
Contoh 1:
Tentukan apakah \(\displaystyle{\sum_{n=1}^\infty} \frac{1}{n} \) divergen atau konvergen.
Pembahasan:
Pertama, kita cari fungsi f(x) di mana \( f(n) =a_n \) sehingga kita peroleh
\[f(x) = \frac{1}{x}\]
Selanjutnya, hitung integral tak wajar untuk fungsi \( f(x) \) yang diperoleh yakni

Karena \(\int_{1}^{\infty} \frac{1}{x} \ dx = \infty \) adalah divergen, maka berdasarkan uji integral, deret \(\displaystyle{\sum_{n=1}^\infty} \frac{1}{n} \) juga divergen.
Contoh 2:
Tentukan apakah \(\displaystyle{\sum_{k=1}^\infty} \frac{k}{e^{k^2}} \) divergen atau konvergen. (Coba gunakan uji divergen dan uji integral)
Pembahasan:
Dengan menggunakan Uji Divergen, maka
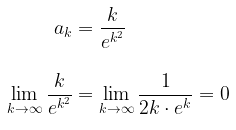
Karena hasil limit sama dengan nol \( = 0\), maka deret bisa divergen atau konvergen (belum dapat disimpulkan). Oleh karena itu, kita tidak bisa menentukan kekonvergenan deret tersebut menggunakan uji divergen. Uji integral akan memberikan jawaban yang kita inginkan.
Dengan menggunakan Uji Integral, maka
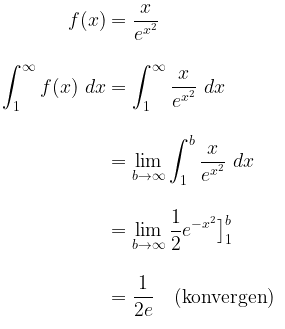
Karena \(\int_{1}^{\infty} \frac{x}{e^{x^2}} \ dx \) konvergen, maka deret \(\displaystyle{\sum_{k=1}^\infty} \frac{k}{e^{k^2}} \) juga konvergen.
Sumber:
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
A person who never made a mistake never tried anything new.
Albert Einstein
