
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Turunan › 20 Contoh Soal Turunan Fungsi Implisit dan Pembahasannya
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
20 Contoh Soal Turunan Fungsi Implisit dan Pembahasannya
Dalam matematika, suatu fungsi dapat dibedakan menjadi fungsi eksplisit dan fungsi implisit. Misalkan terdapat dua variabel yakni \(y\) dan \(x\). Jika hubungan antara \( y \) dan \(x\) dapat dituliskan dalam bentuk fungsi \(y = f(x)\) maka \(y\) disebut fungsi eksplisit dari \(x\), yaitu antara peubah bebas \((x)\) dan tak bebasnya \((y)\) dapat dituliskan dalam ruas yang berbeda. Sebagai contoh, perhatikan beberapa fungsi eksplisit berikut:
\begin{aligned} y &= x^2 + x+ 2 \\[8pt] y &= x^3 - 27 \\[8pt] y &= \frac{x^2-4}{x+2} \\[8pt] y &= \cos x + \sin x \end{aligned}
Sementara itu, fungsi implisit adalah fungsi yang mana variabel tak bebasnya tidak diberikan secara eksplisit dalam bentuk variabel bebasnya. Dalam bahasa lain, fungsi implisit yaitu fungsi yang variabel bebas dan variabel tak bebasnya bercampur dalam satu ruas baik di ruas kanan maupun di ruas kiri. Sebagai contoh, berikut ini adalah beberapa fungsi implisit:
\begin{aligned} (x+y)^3 + (x-y)^3 &= x^4 + y^4 \\[8pt] x^3y^2+x^2+y &= 10 \\[8pt] y^3 &= \frac{x-y}{x+y} \\[8pt] x^3 + y^3 &= 6xy \\[8pt] \sin(xy)+x^2 &= y^2+1 \end{aligned}
Pada artikel ini, kita akan membahas beberapa contoh soal terkait cara mencari turunan atau diferensial dari suatu fungsi implisit. Kita tidak akan masuk ke pembahasan materi mengenai turunan fungsi implisit secara mendetail di sini. Untuk materi mengenai turunan fungsi implisit, kamu dapat membacanya di artikel berikut.

Contoh Soal dan Pembahasan
Sebelum masuk ke contoh soal, sebaiknya kamu sudah mengerti cara mencari turunan dari fungsi eksplisit terlebih dahulu karena itu akan sangat membantu untuk dapat memahami cara mencari turunan fungsi implisit dengan lebih baik.
Contoh 1:
Carilah \( \displaystyle \frac{dy}{dx} \) atau turunan dari fungsi implisit berikut: \( 3 \ln xy + \sin y = x^2 \).
Pembahasan:
Fungsi implisit dalam soal ini bisa disederhanakan terlebih dahulu menjadi:

Selanjutnya, dengan menurunkan kedua ruas persamaan fungsi implisit di atas, kita peroleh:

Contoh 2:
Carilah \( \displaystyle \frac{dy}{dx} \) turunan dari fungsi \( y = (\sin x)^x \).
Pembahasan:
Perhatikan bahwa fungsi dalam soal ini mengandung eksponen yang merupakan variabel sehingga kita tidak bisa menggunakan rumus turunan \( \displaystyle \frac{d}{dx} (x^n) = nx^{n-1} \). Untuk mencari turunan dari fungsi tersebut, kita bisa memberikan logaritma natural pada kedua ruasnya sehingga diperoleh sebuah fungsi implisit.
\begin{aligned} y &= (\sin x)^x \\[8pt] \ln y &= x \ln \sin x \end{aligned}
Selanjutnya, untuk mencari turunan dari fungsi implisit di atas, kita bisa diferensialkan kedua ruas persamaannya, yakni:

Contoh 3:
Tentukan \( \displaystyle \frac{dy}{dx} \) atau turunan dari fungsi implisit berikut: \( (3x+7)^5 = 2y^3 \)
Pembahasan:
Untuk mencari turunan fungsi implisitnya, kita diferensialkan kedua ruas persamaan terhadap \(x\), yakni:
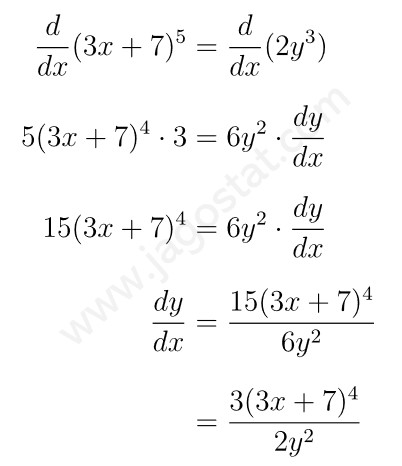
Contoh 4:
Tentukan turunan atau \( \displaystyle \frac{dy}{dx} \) dari fungsi implisit berikut: \[ (x+y)^3+(x-y)^3 = x^4+y^4 \]
Pembahasan:
Untuk mencari turunan dari fungsi implisit dalam soal ini, kita bisa sederhanakan fungsinya terlebih dahulu dengan menguraikan bentuk kubik pada ruas kiri persamaan. Berikut hasil yang diperoleh:

Selanjutnya, dari fungsi implisit yang telah disederhanakan di atas, diferensialkan kedua ruasnya terhadap \(x\), diperoleh:

Contoh 5:
Tentukan \( \displaystyle \frac{dy}{dx} \) atau turunan dari fungsi bentuk implisit berikut: \[ x^3y^2+x^2+y = 10 \]
Pembahasan:
Diferensialkan kedua ruas persamaan pada fungsi implisit, diperoleh:

Contoh 6:
Tentukan \( \displaystyle \frac{dy}{dx} \) atau turunan dari fungsi implisit berikut: \[ \displaystyle y^3 = \frac{x-y}{x+y} \]
Pembahasan:
Perhatikan bahwa kita bisa tuliskan persamaan implisit di atas menjadi:
\begin{aligned} y^3 &= \frac{x-y}{x+y} \\[8pt] y^3(x+y) &= x-y \\[8pt] xy^3+y^4 &= x-y \end{aligned}
Selanjutnya, diferensialkan kedua ruas persamaan implisit di atas terhadap \(x\), yaitu:

Contoh 7:
Tentukan \( \displaystyle \frac{dy}{dx} \) atau turunan fungsi implisit berikut: \[ x^3+5 \ln(xy)-3xy^{-1} = -4 \]
Pembahasan:
Dari sifat logaritma natural, kita tahu bahwa \( 5 \ln(xy) \) dapat juga dituliskan menjadi \( 5 \ln x + 5 \ln y \), sehingga diperoleh:
\begin{aligned} x^3+5 \ln(xy)-3xy^{-1} &= -4 \\[8pt] x^3+5 \ln x + 5 \ln y-3xy^{-1} &= -4 \end{aligned}
Selanjutnya, turunan kedua ruas persamaan fungsi implisit di atas terhadap \(x\), diperoleh:

Baca juga:
Contoh 8:
Tentukan \( \displaystyle \frac{dy}{dx} \) atau turunan dari persamaan implisit: \( y^3 + 7y = x^3 \)
Pembahasan:
Diferensialkan kedua ruas pada persamaan implisit terhadap \(x\), yaitu:
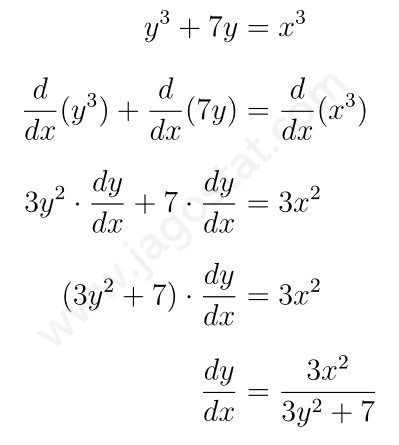
Contoh 9:
Carilah \( \displaystyle \frac{dy}{dx} \) atau turunan fungsi implisit: \( x^2+5y^3 = x+9 \)
Pembahasan:
Diferensialkan kedua ruas pada persamaan implisit terhadap \(x\), yaitu:

Contoh 10:
Carilah \( \displaystyle \frac{dy}{dt} \) atau turunan fungsi implisit berikut: \( t^3 + t^2y-10y^4 = 0 \)
Pembahasan:
Diferensialkan kedua ruas pada persamaan implisit terhadap \(t\), yaitu:

Contoh 11:
Carilah \( \displaystyle \frac{dy}{dx} \) atau turunan dari fungsi implisit: \( x^3 + y^3 = 6xy \)
Pembahasan:
Diferensialkan kedua ruas pada persamaan implisit terhadap \(x\), yaitu:
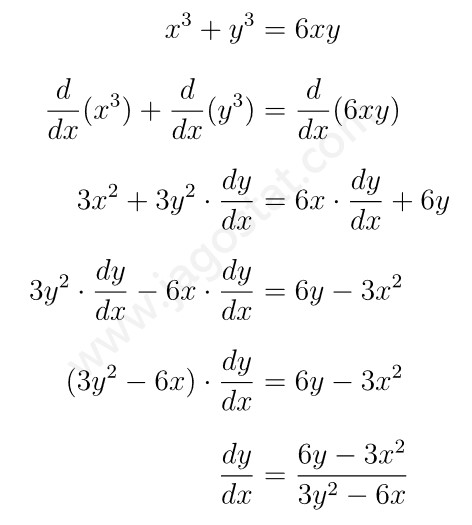
Contoh 12:
Tentukan \( \frac{dy}{dx} \) atau turunan dari bentuk implisit berikut: \[ \sin(xy)+x^2 = y^2 + 1 \]
Pembahasan:
Diferensialkan kedua ruas pada persamaan implisit terhadap \(x\), yaitu:

Contoh 13:
Tentukan turunan pertama atau \( \displaystyle \frac{dy}{dx} \) dari bentuk implisit: \[ x^3-3x^2y+y^2 = 0 \]
Pembahasan:
Diferensialkan kedua ruas pada persamaan implisit terhadap \(x\), yaitu:

Contoh 14:
Tentukan turunan pertama atau \( \displaystyle \frac{dy}{dx} \) dari bentuk implisit: \[ y+\sin(xy) = 1 \]
Pembahasan:
Diferensialkan kedua ruas pada persamaan implisit terhadap \(x\), yaitu:

Contoh 15:
Tentukan turunan pertama atau \( \displaystyle \frac{dy}{dx} \) dari bentuk implisit: \[ \tan(xy)-2y = 0 \]
Pembahasan:
Diferensialkan kedua ruas pada persamaan implisit terhadap \(x\), yaitu:
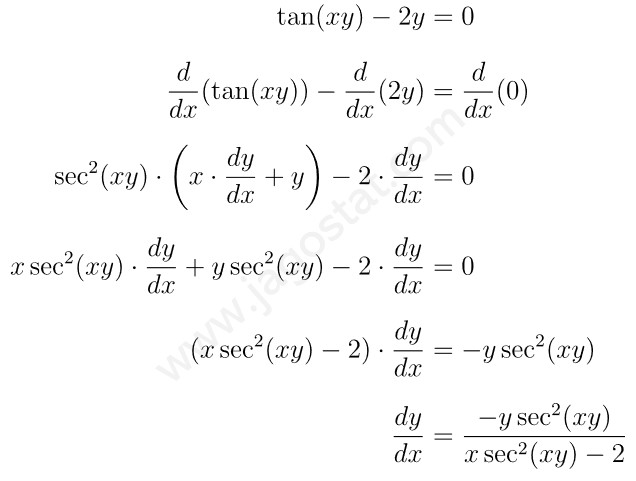
Contoh 16:
Tentukan turunan pertama atau \( \displaystyle \frac{dy}{dx} \) dari bentuk implisit: \[ x^2 \sin(xy)+y = x \]
Pembahasan:
Diferensialkan kedua ruas pada persamaan implisit terhadap \(x\), yaitu:
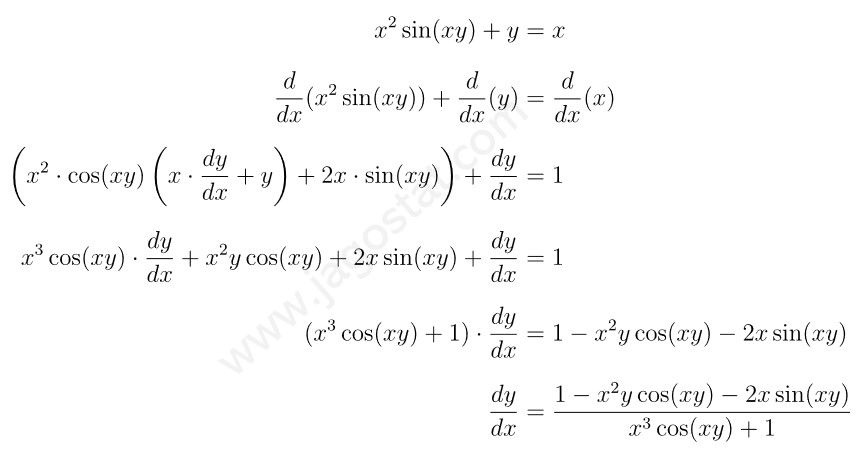
Contoh 17:
Tentukan \( \frac{dy}{dx} \) atau turunan implisit berikut: \( \sin x + \sin y = 0 \)
Pembahasan:
Diferensialkan kedua ruas pada persamaan implisit terhadap \(x\), yaitu:

Contoh 18:
Tentukan \( \frac{dy}{dx} \) atau turunan implisit berikut: \( \sin(x-y) = \cos y \)
Pembahasan:
Diferensialkan kedua ruas pada persamaan implisit terhadap \(x\), yaitu:
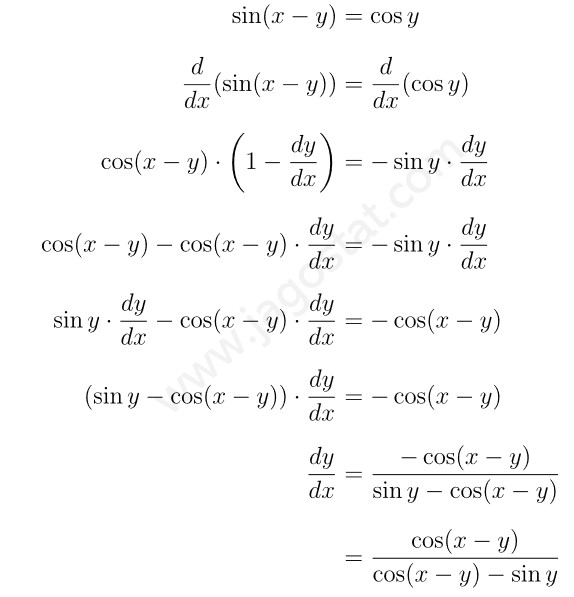
Contoh 19:
Tentukan \( \frac{dy}{dx} \) atau turunan implisit berikut: \( \log(x+y) = x \)
Pembahasan:
Diferensialkan kedua ruas pada persamaan implisit terhadap \(x\), yaitu:

Contoh 20:
Tentukan \( \frac{dy}{dx} \) atau turunan implisit berikut: \( \sqrt{x} + \sqrt{y} = \sqrt{a} \)
Pembahasan:
Diferensialkan kedua ruas pada persamaan implisit terhadap \(x\), yaitu:

Baca juga:
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan jika ada yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
