www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Deret Pangkat, Taylor, dan Mac Laurin › Operasi dalam Deret Pangkat - Materi, Contoh Soal dan Pembahasan
Deret
Operasi dalam Deret Pangkat - Materi, Contoh Soal dan Pembahasan
Deret pangkat berperilaku seperti suku banyak (polinomial) dalam operasi penjumlahan dan pengurangan serta berlaku pula terhadap operasi perkalian dan pembagian.
Pada artikel sebelumnya, kita telah mengetahui bahwa himpunan kekonvergenan deret pangkat \(∑a_n x^n\) adalah sebuah selang \(I\). Selang ini adalah daerah asal sebuah fungsi baru \(S(x)\), yaitu jumlah deret pangkat itu.
Pertanyaan yang wajar ialah, apakah kita dapat menyusun rumus sederhana untuk \(S(x)\) tersebut? Hal ini telah kita lakukan untuk deret geometri, yaitu:

Suatu pertanyaan yang lebih baik diajukan sekarang ialah mengenai sifat-sifat yang dimiliki oleh \(S(x)\). Misalnya, apakah \(S(x)\) dapat didiferensial, apakah dapat diintegralkan? Jawabannya ialah ya untuk kedua pertanyaan tersebut.
Teorema berikut ini mencakup beberapa sifat. Teorema ini mengatakan bahwa \(S\) dapat didiferensialkan dan diintegralkan, dan menunjukkan bagaimana caranya menghitung turunan dan integralnya. Juga mengatakan bahwa radius kekonvergenan deret yang telah didiferensialkan dan deret yang telah diintegralkan sama dengan radius kekonvergenan deret yang asli, walaupun tidak dijelaskan tentang perilaku deret-deret itu di ujung-ujung selang.
Teorema A:
Andaikan \(S(x)\) adalah jumlah sebuah deret pangkat pada sebuah selang \(I\); jadi,

Maka, apabila \(x\) ada di dalam \(I\), berlakulah,

Contoh 1:
Gunakan Teorema A untuk deret geometri
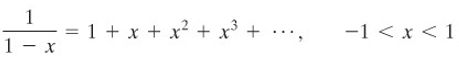
untuk memperoleh rumus-rumus jumlah dua deret baru.
Penyelesaian:
Apabila didiferensialkan suku demi suku, kita peroleh

Sedangkan pengintegralan suku demi suku menghasilkan

Jadi,

Apabila \(x\) kita ganti dengan \(–x\) dan mengalikan ruas kiri dan kanan dengan -1, kita peroleh

Contoh 2:
Tentukan deret pangkat yang menggambarkan \(\tan^{-1}{x}\).
Penyelesaian:
Ingat kembali bahwa

Apabila dalam deret geometri untuk \(1/(1-x)\), \(x\) kita ganti dengan \(-t^2\), kita peroleh

Sehingga,

yaitu,

Contoh 3:
Tentukan rumus untuk jumlah deret

Penyelesaian:
Dari pembelajaran kita sebelumnya, kita lihat bahwa deret tersebut konvergen untuk semua \(x\). Apabila ruas kiri dan kanan kita diferensialkan suku demi suku, kita peroleh

Jadi, \(S'(x)=S(x)\) untuk semua \(x\). Selanjutnya, \(S(0)=1\). Persamaan diferensial ini mempunyai jawaban unik, yaitu \(S(x)=e^x\). Jadi,

Contoh 4:
Tentukan deret pangkat untuk \(e^{-x^2}\)
Penyelesaian:
Apabila dalam deret pangkat untuk \(e^x\), \(x\) kita ganti dengan \(-x^2\), kita peroleh

Operasi-Operasi Aljabar
Deret pangkat berperilaku seperti suku banyak dalam operasi penjumlahan dan pengurangan. Hal ini berlaku pula terhadap operasi perkalian dan pembagian, seperti dalam contoh di bawah ini.
Contoh 5:
Lakukan perkalian dan pembagian deret pangkat untuk \(\ln{(1+x)}\) oleh \(e^x\).
Penyelesaian:
Deret pangkat \(\ln{(1+x)}\) dan \(e^x\) dapat kita lihat pada Contoh 1 dan Contoh 3. Kunci untuk memperkalikan dua deret itu ialah pertama menentukan suku konstanta, kemudian suku \(x\), suku \(x^2\) dan seterusnya. Perkalian itu dapat kita lihat di bawah ini,

Sedangkan, pembagian kita lakukan sebagai berikut.
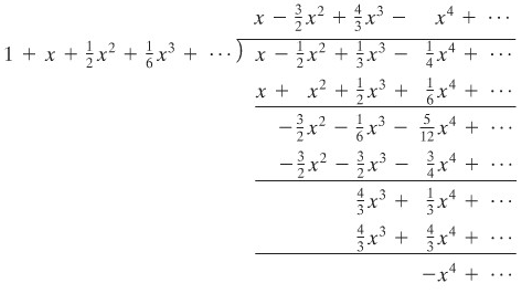
Contoh 6:
Tentukan deret pangkat untuk \(e^{\tan^{-1}{x}}\) hingga suku-suku yang berpangkat 4.
Penyelesaian:
Oleh karena

Kemudian kita substitusikan deret dari \(\tan^{-1}{x}\) (Contoh 2) dan mengumpulkan suku-suku yang sepangkat. Kita peroleh
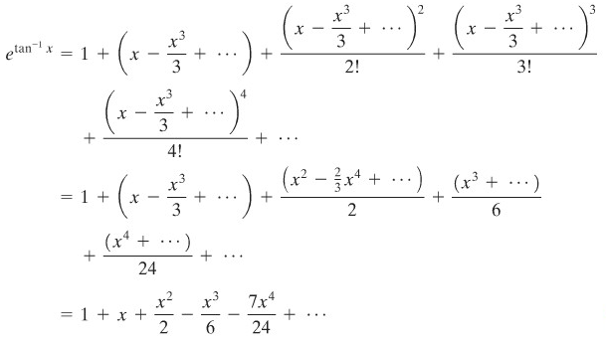
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
Walking with a friend in the dark is better than walking alone in the light.
Helen Keller
