www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Uji Kekonvergenan Deret Tak Hingga › Uji Banding Limit - Materi, Contoh Soal dan Pembahasan
Deret
Uji Banding Limit - Materi, Contoh Soal dan Pembahasan
Uji banding limit (limit comparison test) merupakan salah satu uji kekonvergenan deret tak hingga. Uji ini membandingkan suatu deret tak hingga dengan deret tak hingga yang lain menggunakan limit.
Uji banding limit (limit comparison test) merupakan salah satu uji kekonvergenan deret tak hingga. Pada artikel sebelumnya, kita telah mempelajari uji banding (comparison test), di mana kita tahu bahwa menggunakan uji banding cukup rumit karena perlu menentukan mana deret yang lebih kecil dan yang lebih besar.
Kita bisa mengatasi masalah ini dengan menggunakan uji banding limit. Uji ini membandingkan suatu deret tak hingga dengan deret tak hingga yang lain menggunakan limit.
Teorema: Uji Banding Limit.
Andaikan bahwa \( a_n \geq 0 \) dan \( b_n > 0 \) dan
\[ L = \displaystyle{\lim_{n\to\infty}} \frac{a_n}{b_n} \]
Apabila \( 0 < L < \infty \) maka \( \sum a_n \) dan \( \sum b_n \) bersama-sama akan konvergen atau divergen. Apabila L = 0 dan \( \sum b_n \) konvergen, maka \( \sum a_n \) konvergen.
Contoh 1:
Tentukan apakah deret-deret berikut konvergen atau divergen?
a. \( \displaystyle{ \sum_{i=1}^{\infty} \frac{3n-2}{n^3-2n^2+11} } \)
b. \( \displaystyle{ \sum_{i=1}^{\infty} \frac{1}{\sqrt{n^2+19n}} } \)
Penyelesaian:
Kita gunakan Uji Banding Limit. Untuk ini kita terlebih dahulu harus menentukan pembanding suku ke-n deret ini. Kita harus memeriksa bentuk suku ke-n untuk n yang besar; yang dapat kita tentukan dengan melihat suku-suku derajat tertinggi dalam pembilang dan penyebut suku umum.
Untuk deret (a), suku umumnya mirip dengan \(3/n^2\); untuk deret (b), suku umumnya mirip dengan 1/n.

Jadi, deret pada (a) konvergen dan pada (b) divergen.
Contoh 2:
Apakah \(\displaystyle{\sum_{n=1}^\infty} \frac{\ln{n}}{n^2} \) konvergen atau divergen?
Penyelesaian:
Ke bentuk mana kita akan membandingkan \((\ln{n})/n^2\)? Kalau kita bandingkan dengan \(∑1/n^2\), kita peroleh

Membandingkan dengan \(∑1/n^2\) tampak tidak berhasil; kita coba dengan deret \(∑1/n\). Kita peroleh
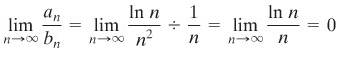
Juga gagal, mungkin dengan deret yang sukunya antara \(1/n^2\) dan \(1/n\) dapat menghasilkan sesuatu. Misalnya \(1/n^{3/2}\). Dalam hal ini

Hasil terakhir ini menggunakan kaidah I’Hopital pada bentuk \(\displaystyle{\lim_{n\to\infty}} \frac{\ln{x}}{\sqrt{x}} \). Menurut bagian kedua Uji Coba Banding Limit, deret \(∑(\ln{n})/n^2\) konvergen oleh karena \(∑1/n^{3/2}\) konvergen.
Contoh 3:
Apakah \( \displaystyle{\sum_{n=1}^{\infty} \frac{n}{n^2+1}} \) konvergen atau divergen?
Pembahasan:
\( \displaystyle{a_n = \frac{n}{n^2+1}} \) dan \( \displaystyle{b_n = \frac{1}{n}}\) (deret harmonik sehingga divergen)

Karena \( L = 1 > 0\) dan terbatas, dan karena \( \displaystyle{ \sum_{n=1}^{\infty} \frac{1}{n}} \) divergen maka deret \( \displaystyle{\sum_{n=1}^{\infty} \frac{n}{n^2+1}} \) juga divergen.
Sumber:
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
If you look at what you have in life, you’ll always have more. If you look at what you don’t have in life, you’ll never have enough.
Oprah Winfrey
