www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Integral Lipat Tiga › Integral Lipat Tiga dalam Koordinat Tabung - Materi, Contoh Soal dan Pembahasan
Integral Lipat
Integral Lipat Tiga dalam Koordinat Tabung - Materi, Contoh Soal dan Pembahasan
Bila suatu benda pejal S di ruang dimensi tiga mempunyai suatu sumbu simetri, perhitungan integral lipat tiga atas S sering kali dipermudah dengan menggunakan koordinat tabung.
Bilamana suatu benda pejal \(S\) di ruang dimensi tiga mempunyai suatu sumbu simetri, perhitungan integral lipat tiga atas \(S\) sering kali dipermudah dengan menggunakan koordinat tabung. Di sini Kita akan membahasnya kenapa bisa demikian.
Sekarang perhatikan Gambar 1 yang mengingatkan kita tentang arti dari koordinat tabung dan memperagakan lambang-lambang yang akan kita gunakan. Koordinat Tabung dan Cartesius (persegi panjang) dihubungkan oleh persamaan-persamaan


Gambar 1.
Sebagai hasil, fungsi \(f(x,y,z)\) ditransformasikan ke
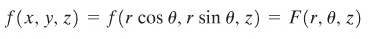
bilamana dituliskan dalam koordinat tabung.
Sekarang andaikan kita bermaksud menghitung \(∭_S f(x,y,z) \ dV\), dengan \(S\) suatu daerah benda pejal. Pandang pemartisian \(S\) memakai suatu kisi tabung, dengan elemen volume khas berbentuk seperti yang diperlihatkan pada Gambar 2. Karena kepingan ini (disebut baji tabung) mempunyai volume \(ΔV_k=\overline{r}_k Δr_k Δθ_k Δz_k\), maka jumlah yang mengaproksimasi integral mempunyai bentuk


Gambar 2.
Pengambilan limit ini untuk norma partisi menuju nol menghasilkan suatu rumus baru dan menyarankan suatu rumus penting untuk perubahan dari koordinat Cartesius ke koordinat tabung dalam suatu integral lipat tiga.
Andaikan \(S\) berupa suatu benda pejal \(z\) sederhana dan andaikan proyeksinya \(S_{xy}\) pada bidang \(xy\) adalah \(r\) sederhana, seperti diperlihatkan pada Gambar 3. Jika \(f\) kontinu pada \(S\), maka

Gambar 3.
Fakta kunci yang harus diperhatikan ialah bahwa \(dz \ dy \ dx\) dari koordinat-koordinat Cartesius menjadi \(r \ dz \ dr \ dθ\) dalam koordinat tabung.
Contoh 1
Tentukan volume daerah pejal \(S\) yang dibatasi di atas oleh paraboloid \(z=4-x^2-y^2\), di bawah oleh \(z = 0\), dan secara menyamping oleh \(y = 0\) dan tabung \(x^2+y^2=2x\), seperti diperlihatkan pada Gambar 5.
Penyelesaian:
Dalam koordinat tabung, paraboloid adalah \(z=4-r^2\) dan tabung adalah \(r=2 \cos θ\). Variabel \(z\) bergerak dari bidang \(xy\) ke atas paraboloid, yaitu dari 0 ke \(4-r^2\). Gambar 6 menunjukkan “footprint” dari benda pejal dalam bidang \(xy\); gambar ini menyatakan bahwa untuk \(θ\) yang tetap, \(r\) bergerak dari 0 ke \(2 \cos θ\). Akhirnya, \(θ\) bergerak dari \(0\) ke \(π/2\). Jadi
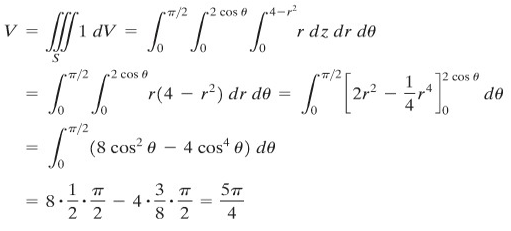

Gambar 5 (Kiri) dan 6 (Kanan).
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
It does not matter how slowly you go as long as you do not stop.
Confucius
