www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Deret Pangkat, Taylor, dan Mac Laurin › Deret Pangkat - Materi, Contoh Soal dan Pembahasan
Deret
Deret Pangkat - Materi, Contoh Soal dan Pembahasan
Ada dua pertanyaan penting mengenai deret fungsi \((∑ u_n (x))\), yaitu: (i) Untuk nilai \(x\) manakah deret itu konvergen? dan (ii) Ke fungsi apakah deret itu konvergen?
Sejauh ini kita telah mempelajari deret-deret yang terdiri atas konstanta-konstanta yang berbentuk \(∑u_n\), dengan \(u_n\) sebuah bilangan. Sekarang kita akan mempelajari deret suatu fungsi yang berbentuk \(∑u_n (x)\). Sebagai contoh, perhatikan deret berikut:

Apabila untuk \(x\) kita substitusikan suatu nilai (misalnya \(x=2,1\)), kita peroleh suatu deret yang terdiri atas konstanta-konstanta yang telah kita pelajari.
Ada dua pertanyaan penting mengenai deret fungsi, yaitu: (i) Untuk nilai \(x\) manakah deret itu konvergen? dan (ii) Ke fungsi apakah deret itu konvergen; atau dengan kata lain, berapakah jumlah \(S(x)\) deret itu?
Sebuah deret pangkat dalam \(x\) mempunyai bentuk:

(\(a_0 x^0\) kita anggap sebagai \(a_0\), juga apabila \(x = 0\)). Untuk deret pangkat ini, kita dapat menjawab dua pertanyaan di atas.
Contoh 1:
Untuk nilai-nilai \(x\) manakah deret pangkat

konvergen dan berapakah jumlahnya? Anggap \(a≠0\).
Penyelesaian:
Deret di atas dinamakan deret geometri. Deret tersebut konvergen untuk \(-1 < x < 1\) dengan jumlah \(S(x)\) yang memenuhi hubungan

Himpunan Kekonvergenan (Convergence Set)
Himpunan bilangan riil yang anggota-anggotanya membentuk suatu deret pangkat konvergen dinamakan himpunan kekonvergenan. Dari Contoh 1 dapat ditarik kesimpulan bahwa himpunan tersebut dapat berbentuk suatu selang terbuka (lihat Gambar 1).

Gambar 1.
Contoh 2:
Tentukan himpunan kekonvergenan deret berikut:
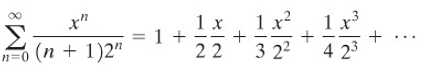
Penyelesaian:
Perhatikan bahwa sekian suku-suku dapat berupa suku-suku negatif (apabila \(x\) negatif). Kita akan menggunakan Uji Hasilbagi Mutlak untuk menyelidiki kekonvergenan mutlak.

Jadi, deret tersebut konvergen mutlak (jadi konvergen) apabila \(ρ=|x|/2<1\) dan divergen apabila \(ρ=|x|/2>1\). Jadi deret konvergen untuk \(|x|<2\) dan divergen untuk \(|x|>2\).
Apabila \(x = 2\) atau \(x = -2\), Uji Hasilbagi gagal. Akan tetapi jika \(x = 2\), deret tersebut adalah deret harmonik yang divergen; sedangkan apabila \(x = -2\), deret ini menjadi deret harmonik ganti-tanda yang konvergen. Sehingga himpunan kekonvergenan deret yang diketahui adalah selang \(-2≤x<2\) (Gambar 2).

Gambar 2.
Contoh 3:
Tentukan himpunan kekonvergenan deret \( \displaystyle{ \sum_{n=0}^∞ \frac{x^n}{n!} }\).
Penyelesaian:
Karena
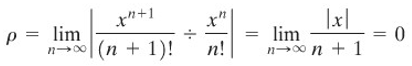
maka berdasarkan Uji Hasilbagi Mutlak, deret konvergen untuk semua \(x\) (Gambar 3)

Gambar 3.
Contoh 4:
Tentukan himpunan kekonvergenan deret \( \displaystyle{ \sum_{n=0}^∞ n!x^n }\).
Penyelesaian:
Karena

Maka, deret konvergen hanya untuk \(x = 0\) (Gambar 4)
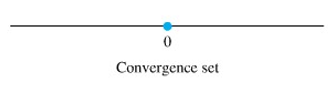
Gambar 4.
Dalam tiap-tiap contoh di atas, himpunan kekonvergenan adalah sebuah selang (dalam contoh terakhir, selang itu menyempit menjadi satu titik). Memang himpunan kekonvergenan itu selalu berbentuk sebuah selang. Tidak mungkin suatu deret pangkat memiliki himpunan kekonvergenan yang terdiri atas dua bagian yang lepas (seperti \([0,1] \ \cup \ [2,3]\)). Sifat ini kita tuangkan dalam teorema berikut.
Teorema A:
Himpunan kekonvergenan sebuah deret pangkat \(∑a_n x^n\) selalu berbentuk selang yang berupa salah satu dari ketiga jenis berikut.
- Satu titik \(x = 0\)
- Selang \((-R, R)\), mungkin ditambah salah satu atau kedua titik ujungnya
- Seluruh himpunan bilangan riil
Dalam (i), (ii), dan (iii), dikatakan bahwa radius kekonvergenan masing-masing adalah \(0, \ R\) dan \(∞\).
Teorema B:
Deret pangkat \(∑a_n x^n\) konvergen mutlak pada bagian dalam selang kekonvergenannya. Pada titik ujungnya deret ini dapat pula konvergen mutlak, tetapi hal ini tidak selalu benar (lihat Contoh 2).
Deret Pangkat Dalam \(x-a\)
Sebuah deret yang berbentuk

dinamakan deret pangkat dalam \(x-a\).
Sifat-sifat yang berlaku bagi deret pangkat dalam \(x\), berlaku pula bagi deret pangkat dalam \(x-a\). Khususnya, himpunan kekonvergenan berbentuk salah satu selang berikut.
- Titik tunggal \(x = a\).
- Selang \((a-R, a+R)\), mungkin ditambah dengan salah satu atau kedua titik ujungnya (Gambar 5)
- Seluruh himpunan bilangan riil.

Gambar 5.
Contoh 5:
Tentukan himpunan kekonvergenan deret \( \displaystyle{ \sum_{n=0}^∞ \frac{(x-1)^2}{(n+1)^2} }\).
Penyelesaian:
Kita gunakan Uji Hasilbagi Mutlak.

Jadi, deret ini konvergen apabila \(|x-1|<1\) , yaitu apabila \(0 < x < 2\); deret ini divergen apabila \(|x-1|>1\). Deret juga konvergen (bahkan konvergen mutlak) pada ujung-ujung selang, yaitu di \(x = 0\) dan \(x = 2\). Hal ini dapat dilihat apabila nilai-nilai tersebut disubstitusikan ke dalam deret. Jadi himpunan kekonvergenan deret adalah selang \([0,2]\) (Gambar 6).

Gambar 6.
Contoh 6:
Tentukan himpunan kekonvergenan untuk
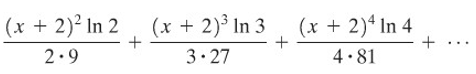
Penyelesaian:
Suku ke-\(n\) adalah \( \displaystyle{ u_n = \frac{(x+2)^n \ln{n}}{n \cdot 3^n} }\)
Jadi,

Kita ketahui deret ini konvergen bila \(p<1\), yaitu bila \(|x+2|<3\) atau \(-5 < x < 1\), tetapi kita harus memeriksa titik-titik ujungnya yaitu – 5 dan 1.
Pada \(x = - 5\).

dan \(∑ (-1)^n (\ln{n})/n\) konvergen berdasarkan Uji Deret Ganti-tanda.
Pada \(x = 1, \ U_n=(\ln{n})/n\) dan \(∑(\ln{n})/n\) divergen berdasarkan pembandingan dengan deret harmonik.
Dapat kita simpulkan bahwa deret tersebut konvergen pada interval \(-5≤x<1\).
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
The greatest discovery of all time is that a person can change his future by merely changing his attitude.
Oprah Winfrey
