www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Integral Lipat Dua › Volume Benda Padat dengan Menggunakan Integral Lipat Dua - Materi, Contoh Soal dan Pembahasan
Integral Lipat
Volume Benda Padat dengan Menggunakan Integral Lipat Dua - Materi, Contoh Soal dan Pembahasan
Setelah benar-benar memahami integral lipat dua dengan pendekatan Riemann yang dibahas pada artikel sebelumnya, sekarang kita bersungguh-sungguh menghadapi masalah perhitungan integral lipat dua \(∬_R f(x,y) \ dA\) dengan R berupa persegi panjang

Misalkan untuk saat ini bahwa \(f(x,y) ≥ 0\) pada \(R\) sehingga kita dapat menafsirkan integral lipat dua sebagai volume \(V\) dari benda pejal di bawah permukaan dari Gambar 1, yakni .

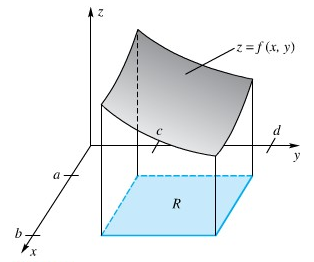
Gambar 1.
Terdapat cara lain untuk menghitung volume benda pejal ini yakni dengan mengiris benda pejal itu menjadi kepingan-kepingan sejajar terhadap bidang \(xz\). Suatu kepingan khas yang demikian diperlihatkan pada Gambar 2(a). Luas muka kepingan ini tergantung pada seberapa jauh ia dari bidang \(xz\), yakni ia tergantung pada \(y\); karena itu, kita nyatakan luas ini oleh \(A(y)\) (lihat Gambar 2(b)).
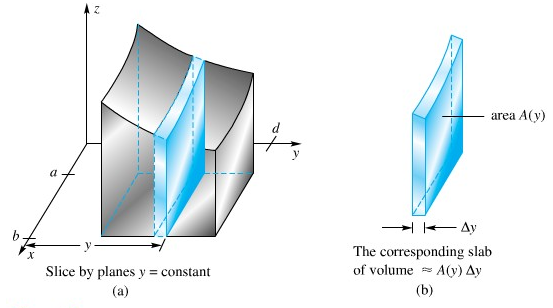
Gambar 2.
Volume ΔV dari kepingan secara aproksimasi diberikan oleh

dan, dengan menggunakan prosedur tiga langkah yang telah kita pelajari pada Kalkulus 1 yakni iris, aproksimasi, integralkan, maka kita boleh menuliskan

Dalam hal lain, untuk \(y\) tetap kita boleh menghitung \(A(y)\) dengan menggunakan integral tunggal biasa; yakni,

Kita simpulkan bahwa
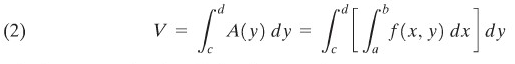
sebuah ekspresi yang disebut integral lipat (integral berulang = iterated integrals).
Bilamana kita menyamakan ekspresi rumus \(V\) dari (1) dan (2), kita peroleh hasil berikut ini.

Jika kita memulai proses di atas dengan cara mengiris benda pejal dengan bidang bidang sejajar bidang yz, kita akan memperoleh integral lipat lain dengan pengintegralan yang berlangsung dalam urutan berlawanan.

Bagaimana Jika F Negatif?
Jika \(f(x,y)\) negatif pada bagian R, maka \(∬_R f(x,y) \ dA\) menghasilkan volume bertanda dari benda padat antara permukaan \(z = f(x,y)\) dan persegi panjang \(R\) dari bidang \(xy\).

Volume sebenarnya benda padat ini adalah

Perhitungan Integral Lipat
Kita mulai dengan sebuah contoh sederhana.
Contoh 1:
Hitunglah integral

Penyelesaian:
Pada integral sebelah dalam \(y\) berupa konstanta, sehingga
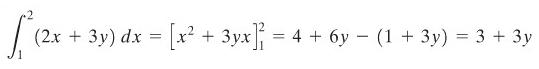
Dengan demikian,
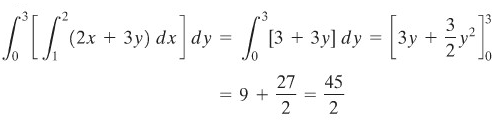
Contoh 2:
Hitunglah integral
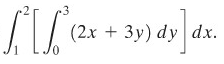
Penyelesaian:
Perhatikan bahwa untuk menjawab soal ini kita cukup menukar urutan pengintegralan dari Contoh 1 dan kita harapkan jawaban yang sama akan diperoleh seperti dalam contoh itu.

Jadi,

Mulai saat ini, biasanya kita akan menghilangkan kurung siku dalam integral lipat, yang membolehkan urutan \(dx \ dy\) atau \(dy \ dx\) untuk memerinci pengintegralan mana yang dilakukan pertama kali. Tentu saja, batas-batas pada tanda integral yang sebelah dalam mengacu peubah pertama yang harus diintegralkan. Perhatikan Contoh 3 berikut.
Contoh 3:
Hitunglah integral
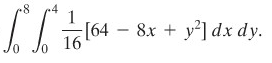
Penyelesaian:
Perhatikan bahwa integral lipat ini telah kita bahas sebelumnya dalam artikel mengenai integral lipat dua atas daerah persegi panjang di mana kita memperoleh jawaban aproksimasi menggunakan integral Riemann sebesar 138. Sekarang kita peroleh nilai eksaknya yaitu 138 2/3.

Penghitungan volume
Sekarang kita dapat menghitung volume untuk aneka-ragam benda pejal.
Contoh 4:
Cari volume \(V\) dari benda pejal yang di atas dibatasi oleh \(z=4-x^2-y^2\) dan di bawah oleh persegipanjang \(R={(x,y):0≤x≤1,0≤y≤2}\) (lihat gambar 3).

Gambar 3.
Penyelesaian:

Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
The greatest pleasure in life is doing what people say you cannot do.
Walter Bagehot
