Contoh 1:

Cari nilai-nilai maksimum atau minimum lokal dari \(f(x,y)=x^2-2x+y^2/4\).

Penyelesaian:

Fungsi yang diberikan dapat didiferensialkan sepanjang daerah asalnya, yaitu bidang \(xy\). Jadi, titik-titik kritis yang mungkin adalah titik-titik stasioner yang diperoleh dengan cara menetapkan \(f_x (x,y)\) dan \(f_y (x,y)\) sama dengan nol.

Tetapi \(f_x (x,y)=2x-2\) dan \(f_y (x,y)=y/2\) adalah nol hanya jika \(x = 1\) dan \(y = 0\). Tinggal memutuskan apakah \((1,0)\) memberikan nilai maksimum atau nilai minimum atau bukan keduanya. Perhatikan bahwa \(f(1,0)=-1\) dan

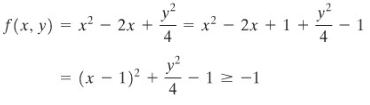
Jadi, \(f(1,0)\) sebenarnya adalah suatu minimum global untuk \(f\). Tidak terdapat nilai-nilai maksimum lokal.

Contoh 2:

Tentukan nilai-nilai minimum atau maksimum lokal dari \(f(x,y)=-x^2/a^2 +y^2/b^2\) .

Penyelesaian:

Titik-titik kritis hanya diperoleh dengan menetapkan \(f_x (x,y)=-2x/a^2\) dan \(f_y (x,y)=2y/b^2\) sama dengan nol. Ini menghasilkan titik \((0,0)\), yang tidak memberikan suatu maksimum atau minimum (lihat Gambar 2). Ini disebut titik pelana (saddle point). Fungsi tersebut juga tidak mempunyai nilai ekstrim lokal.

Gambar 2

Contoh 3:

Tentukan ekstrem, jika ada, untuk fungsi \(F\) yang didefinisikan oleh \(F(x,y)=3x^3+y^2-9x+4y\).

Penyelesaian:

Karena \(F_x (x,y)=9x^2-9\) dan \(F_y (x,y)=2y+4\), maka titik-titik kritis yang diperoleh dengan memecahkan persamaan simultan \(F_x (x,y)=F_y (x,y)=0\) adalah \((1, -1)\) dan \((-1, -2)\).

Sekarang \(F_{xx} (x,y)=18x, \ F_{yy} (x,y)=2\), dan \(F_{xy}=0\). Jadi pada titik kritis (1, -2), kita peroleh

\begin{aligned} D &= F_{xx} (1,-2)⋅F_{yy} (1,-2)-F_{xy}^2 (1,-2 \\[8pt] &= 18(2)-0=36 > 0 \\[8pt] \end{aligned}

Selain itu, karena \(F_{xx} (1,-2)=18>0\), sehingga menurut (ii), \(F(1,-2)=-10\) adalah nilai minimum lokal dari \(F\).

Dalam pengujian fungsi yang diberikan di titik kritis lainnya, \((-1,-2)\) kita dapatkan \(F_{xx} (-1,-2)=-18, \ F_{yy} (-1,-2)=2\), dan \(F_{xy} (-1,-2)=0\), yang menghasilkan \(D=-36<0\). Menurut (ii), \((-1,2)\) adalah titik pelana dan \(F(-1,-2)\) bukan suatu ekstrem.

Contoh 4:

Tentukan jarak minimum antara titik asal dan permukaan \(z^2=x^2 y+4\).

Penyelesaian:

Ambil \(P(x,y,z)\) titik sebarang pada permukaan tersebut. Kuadrat jarak dari titik asal dan \(P\) adalah \(d^2=x^2+y^2+z^2\). Kita mencari koordinat \(P\) yang memberikan \(d^2\) (dan oleh karena itu d) minimum.

Karena \(P\) terletak pada permukaan itu, koordinatnya memenuhi persamaan permukaan. Substitusi \(z^2=x^2 y+4\) pada \(d^2=x^2+y^2+z^2\), kita peroleh \(d^2\) sebagai fungsi dua peubah \(x\) dan \(y\):

Untuk mencari titik kritisnya, kita tetapkan \(f_x (x,y)=0\) dan \(f_y (x,y)=0\), sehingga

Dengan menghilangkan \(y\) dari persamaan-persamaan ini, kita dapatkan

Jadi, \(x = 0\) atau \(x=±\sqrt{2}\). Dengan mensubstitusikan nilai-nilai ini pada persamaan kedua kita peroleh \(y = 0\) dan \(y = -1\). Karena itu, titik-titik kritisnya adalah \((0, 0), \ (\sqrt{2},-1)\) dan \((-\sqrt{2},-1)\).

Untuk menguji masing-masing ini, kita perlukan

\begin{aligned} f_{xx} (x,y) &=2+2y, \\[8pt] f_{yy} (x,y) &=2, \\[8pt] f_{xy} (x,y) &=2x, \\[8pt] D(x,y) &=f_{xx} f_{yy}-f_{xy}^2=4+4y-4x^2 \end{aligned}

Karena \(D(±\sqrt{2},-1)=-8<0\), maka \((\sqrt{2},-1)\) atau \((-\sqrt{2},-1)\) tidak memberikan suatu ekstrem. Tetapi, \(D(0,0) = 4 >0\) dan \(f_{xx} (0,0)=2>0\); sehingga \((0, 0)\) menghasilkan jarak minimum.

Dengan mensubstitusikan \(x = 0\) dan \(y = 0\) ke dalam ekspresi untuk \(d^2\), kita peroleh \(d^2=4\). Jarak minimum antara titik asal dan permukaan yang diberikan adalah 2.