www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Integral Lipat Dua › Integral Lipat Dua Dalam Koordinat Polar - Materi, Contoh Soal dan Pembahasan
Integral Lipat
Integral Lipat Dua Dalam Koordinat Polar - Materi, Contoh Soal dan Pembahasan
Kurva-kurva tertentu seperti lingkaran, kardioid, dan lainnya, lebih mudah diuraikan dalam bentuk koordinat polar sehingga integral lipat dua atas daerah yang dilingkungi oleh kurva-kurva yang demikian lebih mudah dihitung dengan menggunakan koordinat polar.
Kurva-kurva tertentu pada bidang, seperti lingkaran, kardioid, dan lainnya, lebih mudah diuraikan dalam bentuk koordinat polar daripada dalam koordinat Cartesius (persegi panjang). Jadi, kita dapat mengharapkan bahwa integral lipat dua atas daerah yang dilingkungi oleh kurva-kurva yang demikian lebih mudah dihitung dengan menggunakan koordinat kutub.

Gambar 1
Andaikan \(R\) mempunyai bentuk yang diperlihatkan pada Gambar 1, yang kita namakan suatu persegi panjang kutub. Andaikan \(z = f(x,y)\) menentukan suatu permukaan atas \(R\) dan andaikan \(f\) adalah kontinu dan taknegatif. Maka Volume \(V\) dari benda pejal di bawah permukaan ini dan di atas \(R\) (Gambar 2) diberikan oleh


Gambar 2
Dalam koordinat kutub, suatu persegi panjang kutub \(R\) berbentuk

dengan \(a≥0\) dan \(β-α≤2π\). Juga, persamaan permukaan dapat dituliskan sebagai
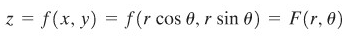
Kita akan menghitung volume \(V\) dengan suatu cara baru yang menggunakan koordinat kutub.
Partisi \(R\) ke dalam persegipanjang kutub yang lebih kecil \(R_1,R_2,…,R_n\) dengan menggunakan suatu kisi kutub dan andaikan \(Δr_k\) dan \(Δθ_k\) menunjukkan ukuran kepingan \(R_k\) yang khas, seperti diperlihatkan pada Gambar 3. Luas \(A(R_k)\) diberikan oleh
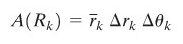
dengan \(\overline{r}_k\) adalah radius rata-rata \(R_k\). Jadi,
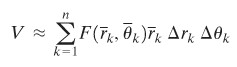

Gambar 3
Bilamana kita mengambil limit untuk norma dari partisi mendekati nol, kita seharusnya memperoleh volume yang sebenarnya. Limit ini adalah suatu integral lipat dua.
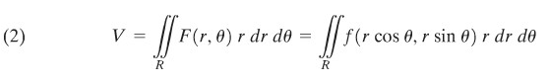
Sekarang kita mempunyai dua rumus untuk \(V\), yakni, (1) dan (2). Dengan menyamakan keduanya dihasilkan

Contoh 1
Tentukan volume \(V\) dari benda padat di atas persegipanjang kutub (Gambar 4).

dan di bawah permukaan \(z = e^{{x^2}+{y^2}}\).
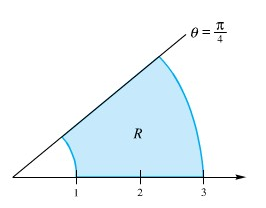
Gambar 4
Penyelesaian:
Karena \(x^2+y^2=r^2\), maka

Tanpa pertolongan koordinat kutub, kita tidak akan pernah menyelesaikan masalah ini. Perhatikan bagaimana faktor tambahan \(r\) adalah apa yang kita perlukan untuk menganti-turunkan \(e^{r^2}\).
Sekarang kita perkenalkan apa yang disebut himpunan \(r\) sederhana dan \(θ\) sederhana dalam pengintegralan kutub. Sebut himpunan \(S\) suatu himpunan \(r\) sederhana jika ia berbentuk (Gambar 5)
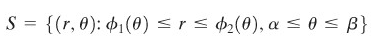
dan disebut \(θ\) sederhana jika ia berbentuk (Gambar 6)


Gambar 5 (Kiri) dan 6 (Kanan)
Contoh 2:
Hitung

di mana S adalah daerah di kuadran pertama yang berada di luar lingkaran \(r = 2\) dan di dalam kardioid \(r=2(1+\cos θ)\) (lihat Gambar 7).
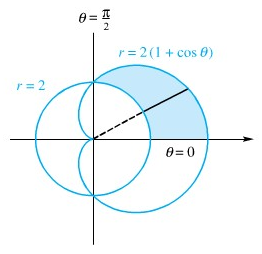
Gambar 7
Penyelesaian:
Karena \(S\) adalah suatu himpunan \(r\) sederhana, kita tuliskan integral yang diberikan sebagai suatu integral lipat kutub, dengan \(r\) sebagai peubah pengintegralan pertama. Dalam pengintegralan sebelah dalam ini, \(θ\) dipertahankan tetap; pengintegralan adalah sepanjang garis tebal dari Gambar 7 mulai dari \(r = 2\) ke \(r=2(1+\cosθ)\).

Contoh 3:
Tentukan volume benda pejal di bawah permukaan \(z=x^2+y^2\), di atas bidang \(xy\), dan di dalam tabung \(x^2+y^2=2y\) (Gambar 8).

Gambar 8
Penyelesaian:
Dari simetri, kita dapat menggandakan volume di oktan pertama. Bilamana kita memakai \(x=r \cosθ\) dan \(y = r \sinθ\), persamaan permukaan menjadi \(z=r^2\) dan persamaan tabung menjadi \(r=2 \sinθ\). Andaikan \(S\) menyatakan daerah yang diperlihatkan pada Gambar 9. Volume \(V\) yang diminta diberikan oleh


Gambar 9
Integral Peluang
Dalam teori peluang dan statistika, kita membahas fungsi kepadatan peluang normal standar

Syarat dari fungsi tersebut yakni \( ∫_\limits{-∞}^∞ f(x) dx=1\). Kita dapat membuktikan bahwa integral tersebut sama dengan 1 dengan menggunakan integral lipat dua dalam koordinat polar. Klik link berikut untuk melihat pembuktiannya.
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
I am thankful to those who said NO to me. It’s because of them I did it myself.
Albert Einstein
