www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Fungsi Peubah banyak › Grafik Fungsi Peubah Banyak
Fungsi
Grafik Fungsi Peubah Banyak
Grafik fungsi dua peubah \(f\) merupakan himpunan semua titik \((x,y,z)\) dengan \(z = f(x,y)\). Biasanya grafik ini merupakan surface atau permukaan.
Grafik fungsi dua peubah \(f\) merupakan himpunan semua titik \((x,y,z)∈R^3\) dengan \(z=f(x,y)\). Biasanya grafik ini merupakan surface atau permukaan (Gambar 1) dan karena setiap \((x,y)\) di daerah asal hanya berpadanan dengan satu nilai \(z\), maka setiap garis tegak memotong permukaan paling banyak di satu titik.

Gambar 1.
Contoh 1:
Sketsa grafik dari \(f(x,y)= \frac{1}{3} \sqrt{(36-9x^2-4y^2)}\)
Penyelesaian:
Andaikan \(z = \frac{1}{3} \sqrt{(36-9x^2-4y^2)}\) dan perhatikan bahwa \(z≥0\). Jika kedua ruas kita kuadratkan dan sederhanakan, kita peroleh persamaan
\[ 9x^2+4y^2+9z^2=36 \]
Persamaan ini kita kenal sebagai persamaan elipsoid. Grafik dari persamaan yang diberikan merupakan sebagian dari permukaan atas elipsoid ini; grafik ini ditunjukkan pada Gambar 2.

Gambar 2.
Contoh 2:
Buatlah sketsa grafik dari \(z=f(x,y)=y^2-x^2\).
Penyelesaian:
Grafiknya merupakan sebuah paraboloid hiperbol dan sketsanya pada Gambar 3.

Gambar 3.
Sejumlah perangkat lunak komputer termasuk Maple dan Mathematica, telah dibuat untuk menghasilkan grafik tiga dimensi dengan mudah. Berikut ini 4 grafik yang dibuat dengan bantuan perangkat lunak komputer.

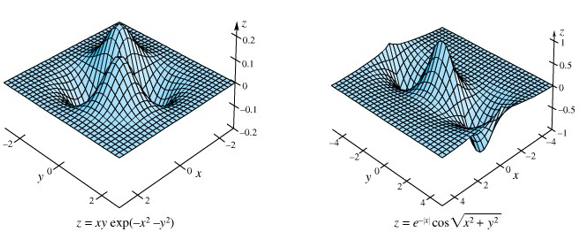
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
A friend is someone who knows all about you and still loves you.
Elbert Hubbard
