www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Transformasi Koordinat › Transformasi Koordinat dalam Integral Lipat - Materi, Contoh Soal dan Pembahasan
Integral Lipat
Transformasi Koordinat dalam Integral Lipat - Materi, Contoh Soal dan Pembahasan
Kita namakan penggantian peubah (change of variables) ini sebagai transformasi. Sering kali, alasan mengganti peubah adalah untuk memperoleh integral yang bisa dikerjakan dengan peubah baru tersebut.
Sering kali, kita perlu menghitung integral lipat dua atau lipat tiga dalam sebuah sistem koordinat selain sistem koordinat-\(xy\). Ini mungkin dilakukan baik karena bentuk daerah pengintegralan yang rumit maupun karena kompleknya fungsi integran dalam suatu integral. Mengubah integral lipat dalam suatu sistem koordinat baru akan membantu dalam menyederhanakan penghitungan.
Penggantian Peubah/Variabel (Change of Variables)
Anda mungkin masih ingat pelajaran dalam Kalkulus 1 bahwa teknik substitusi untuk mencari integral dapat dinyatakan dengan

Perhatikan bahwa kita mengambil integral dalam bentuk peubah \(x\) dan mengubahnya menjadi integral dalam bentuk peubah \(u\). Sebagai contoh, untuk mengerjakan integral

kita substitusi \(u=g(x)=x^2-4\), maka \(du = 2x \ dx\) atau \(x \ dx = ½ \ du\) dan batas pengintegralan berubah yaitu \(u=g(2)=2^2-4=0\) dan \(u=g(3)=3^2-4=5\). Oleh karena itu, integral aslinya diubah menjadi

Tentu saja, integral terakhir dalam bentuk peubah \(u\) lebih mudah dihitung. Dengan kata lain, ketika menyelesaikan masalah integral, kita membuat substitusi yang tepat untuk memperoleh integral yang menjadi lebih sederhana daripada bentuk integral aslinya (original integral).
Kita namakan penggantian peubah (change of variables) ini sebagai transformasi. Sering kali, alasan mengganti peubah adalah untuk memperoleh integral yang bisa dikerjakan dengan peubah baru tersebut. Alasan lainnya yaitu untuk mengubah daerah pengintegralan yang kompleks menjadi daerah yang lebih sederhana untuk dikerjakan.
Kita akan melakukan hal yang serupa untuk integral lipat dua dan lipat tiga. Sebenarnya, kita telah melakukan hal ini saat kita mengubah integral lipat dua ke koordinat polar dan saat kita mengubah integral lipat tiga ke koordinat tabung dan bola. Hanya saja, saat itu kita belum menjelaskan secara detail darimana rumus tersebut berasal.
Rumus untuk mengganti peubah diberikan oleh

di mana: \(x = x(u,v), \ y = y(u,v)\), \(S\) adalah daerah pengintegralan baru hasil transformasi dan

disebut jacobian transformasi \((x,y) → (u,v)\).
Misalkan bahwa transformasi \((x,y) → (u,v)\) adalah pemetaan satu-satu dari \(R\) ke daerah \(S\), hubungan invers dijelaskan oleh Jacobian.

Oleh karena itu, penggunakan penggantian peubah dalam integral lipat dua memerlukan tiga langkah berikut:
- Cari daerah S dalam sistem koordinat baru \((u,v)\) untuk daerah awal pengintegralan R;
- Hitunglah Jacobian transformasi \((x,y) → (u,v)\) dan tuliskan turunannya (diferential) terhadap variabel baru:
- Ganti \(x\) dan \(y\) dalam integran dengan substitusi \(x = x(u,v)\) dan \(y = y(u,v)\).

Contoh 1:
Hitunglah integral lipa dua \[∬_R (y-x) \ dx \ dy\] di mana daerah R dibatasi oleh \[y = x + 1, \ y = x – 3, \ y = - \frac{x}{3} + 2, \ y = - \frac{x}{3} + 4\].
Pembahasan:
Pertama, kita lukiskan daerah R seperti tampak pada Gambar 1.

Gambar 1.
Kita menggunakan penggantian variabel (change of variables) untuk menyederhanakan perhitungan integral. Dengan memisalkan \(u = y – x\) dan \(v = y + x/3\), kita peroleh
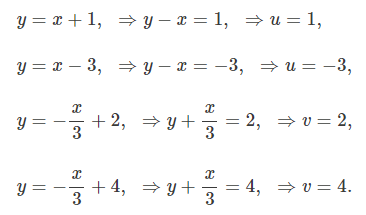
Dengan demikian, daerah hasil transformasi \(S\) adalah persegi panjang seperti tampak pada Gambar 2.

Gambar 2.
Selanjutnya, kita perlu menghitung jacobian.

Nilai mutlak jacobiannya adalah

Dan turunannya yaitu
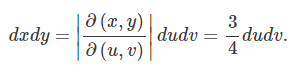
Seperti yang dapat kita lihat bahwa penghitungan integral dengan variabel baru \(u\) dan \(v\) adalah jauh lebih mudah untuk dilakukan.

Contoh 2:
Dengan menggunakan penggantian variabel (change of variables) \(u = x – y\) dan \(v = x + y\), hitunglah
\[ \iint_R (x-y)e^{x^2-y^2} \ dA \]
di mana R adalah daerah yang dibatasi oleh garis \(x + y = 1\) dan \(x + y = 3\) dan kurva \(x^2-y^2=-1\) dan \(x^2-y^2=1\).
Pembahasan:
Pertama, kita temukan daerah R dan gambarkan transformasinya sehingga menjadi lebih mudah untuk mendapatkan limit pengintegralan setelah transformasi dibuat.

Gambar 3. Transformasi daerah R menjadi daerah S untuk menyederhanakan penghitungan integral.
Mengingat \(u = x – y\) dan \(v = x + y\), kita peroleh
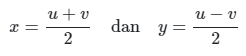
dan karena itu transformasi yang digunakan adalah

Garis \(x + y = 1\) dan \(x + y = 3\) masing-masing menjadi \(v = 1\) dan \(v = 3\). Kurva \(x^2-y^2=1\) dan \(x^2-y^2=-1\) masing-masing menjadi \(uv = 1\) dan \(uv = -1\).
Dengan demikian, kita bisa jelaskan daerah S (lihat daerah kedua pada Gambar 3) sebagai

Jacobian untuk transformasi ini adalah
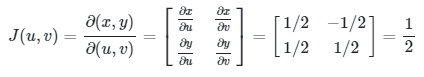
Sehingga dengan menggunakan transformasi T, integral yang akan kita hitung berubah menjadi

Dari hasil perhitungan, kita peroleh

Contoh 3:
Selesaikanlah \(∬_R x+y \ dA\) dengan menggunakan transformasi \(x = 2u + 3v\) dan \(y = 2u – 3v\) jika diketahui R adalah daerah trapesium dengan titik-titik puncak (verticed) diberikan oleh (0,0), (5,0), (5/2, 5,/2), dan (5/2, -5/2).
Pembahasan:
Pertama, kita gambarkan daerah R dan tentukan persamaan untuk tiap-tiap sisi trapesiumnya.

Tiap-tiap persamaan dapat diperoleh berdasarkan informasi dua titik pada tiap garis. Sebenarnya, kita bisa mencari integral lipat dua ini dalam bentuk x dan y, akan tetapi itu akan melibatkan penghitungan dua integral. Oleh karena itu, daripada menghitung dua integral lebih baik kita menyelesaikan integral ini dengan menggunakan transformasi koordinat untuk tiap-tiap persamaan di atas.
Mari kita mulai dari proses transformasi persamaan \(y = x\).
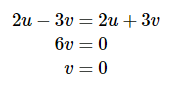
Transformasi serupa dapat dilakukan untuk \(y = -x\), yakni
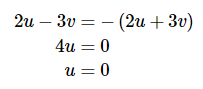
Selanjutnya, kita akan melakukan transformasi persamaan \(y = -x + 5\). Kita peroleh

Terakhir, transformasi \(y = x – 5\) memberikan

Dengan demikian, daerah transformasi S berupa persegi panjang dengan sisi-sisinya diberikan oleh \(u = 0, \ v = 0, \ u = 5/4\) dan \(v = 5/6\). Dengan demikian, range dari \(u\) dan \(v\) yaitu

Berikutnya, kita perlu mencari jacobian yakni

Dengan demikian, kita peroleh

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
When one door of happiness closes, another opens, but often we look so long at the closed door that we do not see the one that has been opened for us.
Helen Keller
