www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Uji Kekonvergenan Deret Tak Hingga › Definisi Kekonvergenan Deret - Materi, Contoh Soal dan Pembahasan
Deret
Definisi Kekonvergenan Deret - Materi, Contoh Soal dan Pembahasan
Dalam mempelajari deret tak hingga, selalu muncul dua pertanyaan penting. Pertama, apakah deret itu konvergen? Kedua, apabila deret tersebut konvergen, berapakah jumlahnya?
Dalam mempelajari deret tak hingga, selalu muncul dua pertanyaan penting. Pertama, apakah deret itu konvergen? Kedua, apabila deret tersebut konvergen, berapakah jumlahnya? Kekonvergenan suatu deret tak hingga ditentukan dari barisan jumlah-jumlah parsial {Sn} dari deret tersebut. Lalu, apa itu barisan jumlah parsial dari suatu deret?
Untuk menjelaskan barisan jumlah parsial, akan lebih baik jika dimulai dengan menperkenalkan barisan tak hingga yang dinotasikan dengan \(\{a_n\}_{n=1}^∞\). Perhatikan bahwa kita memulai barisan pada \(n = 1\) untuk tujuan kemudahan, tapi dalam kenyataannya ia bisa mulai dari berapa saja. Kita telah mempelajari barisan tak hingga, jadi harusnya topik itu bukanlah masalah di sini.
Sekarang, kita akan mendefinisikan jumlah deret parsial sebagai

yang mana ini membentuk suatu barisan baru, kita notasikan \(\{s_n\}_{n=1}^∞\).
Sebuah deret tak hingga adalah limit dari barisan jumlah parsial tersebut, atau kita nyatakan sebagai

Jika barisan jumlah parsial tersebut adalah barisan yang konvergen yakni limitnya ada dan terhingga, maka deret tak hingga tersebut dikatakan konvergen dan dalam kasus ini jika \( \lim_\limits{n\to ∞} s_n = s \) maka \(∑_\limits{i=1}^∞ a_i = s\). Sebaliknya, jika barisan jumlah parsial tersebut adalah barisan yang divergen yakni limitnya tidak ada dan tak hingga, maka deret tak hingga tersebut dikatakan divergen.
Mari kita lihat beberapa contoh bagaimana menentukan kekonvergenan dan kedivergenan suatu deret tak hingga berikut ini.
Contoh 1:
Tentukanlah apakah deret berikut merupakan deret yang konvergen atau divergen. Jika konvergen, tentukanlah nilainya.
\[ \sum_{n=1}^∞ n \]
Pembahasan:
Untuk menentukan apakah deret ini konvergen, kita pertama perlu menemukan bentuk umum untuk barisan jumlah parsialnya, yakni

Karena ini merupakan deret yang cukup terkenal, maka tentu saja kita bisa menemukan bentuk umumnya dengan mudah, yaitu

Sehingga, untuk menentukan apakah deret tersebut konvergen atau tidak, kita perlu mengetahui apakah barisan jumlah parsial
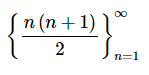
adalah konveren atau divergen. Ini bukanlah pekerjaan sulit karena limit dari bentuk barisan ini adalah

Karena barisan jumlah parsial divergen ke \(∞\), dengan demikian deret juga divergen.
Contoh 2:
Tentukanlah apakah deret berikut merupakan deret yang konvergen atau divergen. Jika konvergen, tentukanlah nilainya.
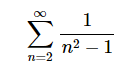
Pembahasan:
Rumus umum untuk jumlah parsial deret tak hingga ini adalah

Dan dalam kasus ini, kita peroleh

Karena barisan jumlah parsial adalah konvergen, maka deret tak hingga ini juga konvergen dan nilainya yaitu

Contoh 3:
Tentukanlah apakah deret berikut merupakan deret yang konvergen atau divergen. Jika konvergen, tentukanlah nilainya.

Pembahasan:
Dalam kasus ini, kita tidak perlu rumus umum untuk jumlah parsialnya dalam menentukan kekonvergenan deret tak hingga ini. Kita tuliskan saja beberapa jumlah parsial pertamanya yakni

Tampaknya barisan jumlah parsialnya adalah

Dan barisan ini adalah divergen karena \( \lim_\limits{n→∞} s_n \) tidak ada. Oleh karena itu, deret tak hingga tersebut adalah divergen.
Contoh 4:
Tentukanlah apakah deret berikut merupakan deret yang konvergen atau divergen. Jika konvergen, tentukanlah nilainya.

Pembahasan:
Rumus umum untuk jumlah parsial deret tak hingga ini aadalah

Dalam kasus ini, limit dari jumlah parsialnya yaitu
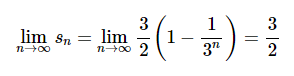
Karena barisan jumlah parsialnya konvergen, maka deret juga konvergen dan nilainya adalah
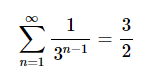
Dari beberapa contoh yang diberikan di atas, untuk menentukan kekonvergenan deret maka kita perlu mencari rumus bentuk umum dari jumlah parsial deret tersebut. Sebagian besar pasti akan setuju bahwa menemukan rumus bentuk umum dari jumlah parsial bukanlah perkara yang mudah.
Faktanya pada bagian selanjutnya kita tidak akan melakukan banyak hal dengan jumlah parsial deret karena kesulitan yang dihadapi dalam menemukan rumus umum. Ini juga berarti bahwa kita tidak akan melakukan banyak pekerjaan dengan nilai deret karena untuk mendapatkan nilai tersebut kita juga perlu mengetahui rumus umum untuk jumlah parsial.
Sekarang mari kita ingat kembali bahwa dari 4 contoh yang diberikan dua di antaranya merupakan deret tak hingga yang konvergen dan duanya lagi adalah deret tak hingga yang divergen.

Perhatikan bahwa untuk dua deret yang konvergen, limit dari bentuk deret tersebut adalah nol. Ini akan selalu benar untuk deret tak hingga yang konvergen. Kita nyatakan dalam teorema berikut:
Teorema:
Jika \(∑ a_n\) konvergen maka \( \lim_\limits{n→∞} a_n = 0 \).
Berhati-hatilah untuk tidak menyalahgunakan teorema ini! Teorema ini memberi kita persyaratan untuk konvergensi tetapi bukan jaminan konvergensi. Dengan kata lain, kebalikan dari teorema ini TIDAK BENAR. Jika \( \lim_\limits{n→∞} a_n = 0 \), deret tersebut mungkin saja divergen. Perhatikan dua contoh deret tak hingga berikut

Dalam dua kasus, bentuk deret adalah nol dalam limitnya ketika n menuju tak hingga. Namun hanya deret kedua yang konvergen sedangkan deret yang pertama adalah divergen.
Sekali lagi bahwa seperti yang dinyatakan di atas, teorema ini memberikan persyaratan untuk kekonvergenan. Agar deret tak hingga konvergen, maka bentuk deret tersebut harusnya menuju nol dalam limitnya. Jika bentuk deret tak menuju nol dalam limitnya, maka tidak ada cara untuk menentukan apakah deret tersebut konvergen.
Ini membawa kita pada salah satu dari beberapa uji kekonvergenan deret tak hingga yang akan kita bahas yakni uji divergen. Kita tuliskan dalam artikel terpisah untuk uji divergen ini. Klik link berikut untuk melanjutkan: Uji Divergen
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
I haven’t failed. I’ve just found 10,000 ways that won’t work.
Thomas Edison
