www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Uji Kekonvergenan Deret Tak Hingga › Uji Konvergen Bersyarat - Materi, Contoh Soal dan Pembahasan
Deret
Uji Konvergen Bersyarat - Materi, Contoh Soal dan Pembahasan
Deret \(∑ u_n\) dinamakan konvergen bersyarat (conditionally convergent) apabila \(∑ u_n\) konvergen, tetapi deret \(∑|u_n|\) divergen. Deret harmonik ganti tanda adalah salah satu contoh deret yang konvergen bersyarat.
Oleh Tju Ji Long · Statistisi
Hub. WA: 0812-5632-4552
Sebuah deret \(∑u_n\) dikatakan konvergen mutlak jika \(∑|u_n|\) adalah konvergen. Sebaliknya, deret \(∑u_n\) dinamakan konvergen bersyarat (conditionally convergent) apabila \(∑u_n\) konvergen, tetapi deret \(∑|u_n|\) divergen. Deret harmonik ganti tanda adalah salah satu contoh deret yang konvergen bersyarat.
Contoh 1:
Buktikan bahwa \(\displaystyle{\sum_{n=1}^\infty (-1)^{n+1} \frac{1}{\sqrt{n}}} \) konvergen bersyarat.
Penyelesaian:
Perhatikan bahwa
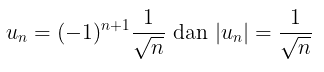
Deret \(\displaystyle{\sum_{n=1}^\infty} (-1)^{n+1} \frac{1}{\sqrt{n}} \) konvergen dengan menggunakan Uji Deret Ganti-Tanda.
Akan tetapi, deret \(\displaystyle{\sum_{n=1}^\infty} \frac{1}{\sqrt{n}} \) divergen, karena bentuk ini adalah deret-\(p\) dengan \(p = ½\).
Dengan demikian, karena \(∑u_n\) konvergen dan \(∑|u_n|\) divergen, maka deret \(\displaystyle{\sum_{n=1}^\infty (-1)^{n+1} \frac{1}{\sqrt{n}}} \) konvergen bersyarat.
Sumber:
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
Anyone who stops learning is old, whether at twenty or eighty. Anyone who keeps learning stays young. The greatest thing in life is to keep your mind young.
Henry Ford