Contoh 1

Buktikan bahwa \(\displaystyle{\sum_{n=1}^\infty} \ \frac{n^3}{3n^3+2n^2} \) adalah deret tak hingga yang divergen.

Penyelesaian:

Perhatikan bahwa

maka menurut Teorema A , deret tersebut divergen.

Contoh 2

Tentukan apakah deret \(\displaystyle{\sum_{n=1}^\infty} \frac{n}{n+1} \) konvergen atau divergen.

Pembahasan:

Perhatikan bahwa

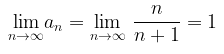
yang mana tidak sama dengan nol (\( \neq 0\)), maka deret \(\displaystyle{\sum_{n=1}^\infty} \frac{n}{n+1} \) divergen.

Contoh 3

Tentukan apakah deret \(\displaystyle{\sum_{n=1}^\infty} \left(\frac{1}{n} - \frac{1}{n+1}\right) \) konvergen atau divergen.

Pembahasan:

Perhatikan bahwa

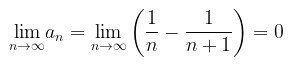
yang mana sama dengan nol, maka deret \(\displaystyle{\sum_{n=1}^\infty} \left(\frac{1}{n} - \frac{1}{n+1}\right) \) bisa divergen atau konvergen. Dengan kata lain, kita belum dapat menyimpulkan apakah deret tersebut divergen atau konvergen berdasarkan Uji Kedivergenan yang diberikan pada Teorema A. Untuk mengetahui apakah deret tersebut konvergen atau divergen, maka perlu dilakukan uji kekonvergenan deret tak hingga yang lain.