www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Limit dan Kekontinuan Fungsi Peubah Banyak › Limit Fungsi Peubah Banyak - Materi, Contoh Soal dan Pembahasan
Limit
Limit Fungsi Peubah Banyak - Materi, Contoh Soal dan Pembahasan
Untuk limit fungsi peubah banyak terdapat tak terhingga banyaknya jalur yang bisa diambil untuk \((x,y) → (a,b)\). Ini berbeda dengan limit fungsi satu peubah yang hanya terdapat dua jalur untuk \(x → a\).
Pada artikel ini kita akan membahas bagaimana mencari limit untuk fungsi lebih dari satu variabel (peubah). Dalam pembahasan limit untuk fungsi satu peubah, kita tahu bahwa limit fungsi satu peubah yang dilambangkan dengan \( \lim_\limits{x\to c} f(x) = L \) mempunyai arti bahwa untuk \(x\) mendekati nilai \(c\), maka \(f(x)\) mendekati nilai \(L\), asalkan limit kiri sama dengan limit kanannya, yakni:
\[ \lim_{x\to c^+} f(x) = \lim_{x\to c^-} f(x) = L \]
Jadi, dengan kata lain, kita mempunyai limit \( \lim_\limits{x\to c} f(x) = L \) asalkan \(f(x)\) mendekati \(L\) ketika bergerak terhadap \(x\) dari kedua sisi, yakni dari sebelah kiri dan kanan nilai \(x\).
Perhatikan bahwa dalam limit fungsi satu peubah hanya terdapat dua jalur yang bisa diambil ketika kita bergerak menuju \(x = a\), yakni kita bisa bergerak dari sebelah kiri atau sebelah kanan nilai \(x\). Kemudian, agar limit fungsi satu peubah ada (exist), maka fungsi tersebut harus mendekati nilai yang sama dengan limit fungsi ketika kita mengambil masing-masing jalur terhadap \(x = a\).
Konsep yang sama berlaku bagi limit untuk lebih dari satu peubah, kecuali kali ini akan terdapat banyak hal yang perlu dilakukan. Tujuan kita sekarang adalah memberikan arti pada lambang limit untuk dua peubah berikut ini:
\[ \lim_{(x,y)\to(a,b)} f(x,y) = L \]
Lambang ini mempunyai arti bahwa nilai \(f(x,y)\) semakin dekat ke bilangan \(L\) pada waktu \((x,y)\) mendekati \((a,b)\). Masalahnya adalah bahwa \(f(x,y)\) dapat mendekati \((a,b)\) dengan cara yang tak terhingga banyaknya (Gambar 1). Tentu, ini berbeda dengan limit fungsi satu peubah yang hanya terdapat dua jalur untuk \(x \to a\), sedangkan untuk limit fungsi lebih dari satu peubah terdapat tak terhingga banyaknya jalur yang bisa diambil untuk \((x,y) \to (a,b)\).

Gambar 1.
Untuk lebih jelasnya, perhatikan definisi untuk limit fungsi peubah banyak berikut ini.
Definisi:
Untuk mengatakan bahwa \( \displaystyle{\lim_{(x,y)\to(a,b)} f(x,y) = L} \) berarti bahwa untuk setiap \(ε>0\) (betapapun kecilnya) terdapat \(δ>0\) yang berpadanan sedemikian sehingga \(|f(x,y)-L|<ε\) dengan syarat bahwa \(0<|(x,y)-(a,b)|<δ\).
Untuk menafsirkan \(|(x,y)-(a,b)|\), bayangkan \((x,y)\) dan \((a,b)\) sebagai vektor-vektor. Maka

dan titik-titik yang memenuhi \(0<|(x,y)-(a,b)|<δ\) adalah titik-titik di dalam suatu lingkaran dengan radius \(δ\) terkecuali pusat \((a,b)\) (Lihat Gambar 2).

Gambar 2.
Dari definisi di atas, kita peroleh beberapa hal berikut ini.
- Jika jalur pendekatan yang berbeda menuju nilai-nilai \(L\) yang berlainan, maka limit tidak ada.
- Fungsi \(f(x,y)\) tidak harus terdefinisi di \((a,b)\). Ini sebagai akibat pembatasan \(0<|(x,y)-(a,b)|\).
- Definisi di atas dapat langsung diperluas ke fungsi tiga peubah (atau lebih). Cukup menggantikan \((x,y)\) dan \((a,b)\) dengan \((x,y,z)\) dan \((a,b,c)\).
Berikut diberikan teorema penting yang berguna terkait limit untuk fungsi lebih dari satu peubah.
Teorema A:
Jika \(f(x,y)\) adalah suatu polinomial, maka

dan jika \(f(x,y)=p(x,y)/q(x,y)\), di mana \(p\) dan \(q\) adalah polinomial, maka

asalkan \(q(a,b)≠0\). Lebih lanjut, jika

maka

tidak ada.

Contoh Soal dan Pembahasan
Setelah mempelajari dan memahami materi mengenai limit fungsi beberapa variabel di atas, sekarang kita akan latihan mengerjakan soal-soal untuk mencari limit dari fungsi beberapa variabel.
Contoh 1:
Hitunglah limit berikut jika ada:

Penyelesaian:
Fungsi yang akan kita cari adalah suatu polinomial, sehingga berdasarkan Teorema A, maka

Contoh 2:
Hitunglah limit berikut jika ada:

Penyelesaian:
Dalam kasus ini fungsi tidak akan kontinu sepanjang garis y = -x karena penyebut pada fungsi tersebut akan bernilai nol dan akibatnya kita akan peroleh pembagian oleh nol. Namun, kita tidak perlu mempermasalahkan ini karena titik yang akan dicari limitnya tidak pada garis tersebut.
Jadi, kita hanya perlu memasukkan nilai titik yang akan dicari limitnya ke fungsi yang diberikan. Kita peroleh berikut ini.

Contoh 3:
Hitunglah limit berikut jika ada:

Penyelesaian:
Dalam kasus ini fungsi tidak kontinu pada titik yang ditanyakan yakni pada titik (1,1) karena kita akan berhadapan dengan pembagian oleh nol. Namun, ini tidak berarti bahwa limit tersebut tidak ada. Kita banyak melihat contoh yang seperti ini pada Kalkulus 1 di mana fungsi yang diberikan tidak kontinu pada titik yang kita cari, tapi limitnya ternyata ada.
Di sini, kita bisa menfaktorkan baik pembilang dan penyebut, sehingga kita peroleh berikut ini.

Contoh 4:
Perlihatkan bahwa fungsi \(f\) yang didefinisikan oleh

tidak mempunyai limit di titik asal.
Penyelesaian:
Fungsi \(f\) didefinisikan di mana saja di bidang \(xy\) kecuali pada titik yang ditanyakan yakni di titik asal atau di titik (0,0). Perhatikan bahwa tidak seperti pada contoh sebelumnya, di sini kita tidak bisa melakukan pemfaktoran sehingga limit bisa diperoleh.
Jika kita bisa mencari dua jalur berbeda untuk mendekati titik yang menghasilkan nilai limit berbeda maka kita simpulkan bahwa limit tersebut tidak ada. Dua jalur umum yang biasa diambil adalah jalur sepanjang sumbu-x dan sumbu-y.
Limit \(f(x,y)\) untuk \((x,y)\) mendekati \((0,0)\) sepanjang sumbu \(x\) adalah

Serupa dengan itu, limit \(f(x,y)\) untuk \((x,y)\) mendekati \((0,0)\) sepanjang sumbu \(y\) adalah
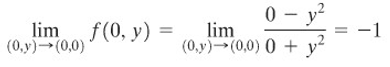
Jadi, kita mendapat jawaban berbeda yang tergantung bagaimana \((x,y)→(0,0)\). Oleh karena itu, kita simpulkan bahwa limit tidak dapat terwujud.
Contoh 5:
Hitunglah limit berikut jika ada:

Penyelesaian:
Perhatikan bahwa fungsi tidak terdefinisi pada titik yang ditanyakan yakni pada titik (0,0) sehingga kita tidak bisa menggantikan nilai titik pada fungsi yang diberikan. Selain itu, kita juga tidak bisa melakukan pemfaktoran di sini. Seperti pada Contoh 4, kita akan mencari dua jalur untuk mendekati titik yang memberikan nilai berbeda pada limit. Kita gunakan jalur sepanjang sumbu-x dan sumbu-y.
Jika kita mendekati (0,0) sepanjang sumbu x, maka y = 0 sehingga

Jadi, sepanjang sumbu-x fungsi akan mendekati nol ketika kita bergerak terhadap titik asal (0,0).
Sementara itu, jika kita mendekati (0,0) sepanjang sumbu y, maka x = 0 sehingga

Jadi, kita peroleh nilai limit yang sama.
Perlu kehati-hatian di sini. Meskipun kedua jalur yang kita ambil memberikan nilai limit yang sama bukan berarti limit tersebut ada dan mempunyai nilai nol. Hasil yang kita peroleh hanya memberikan arti bahwa limit mempunyai nilai yang sama sepanjang dua jalur tadi.
Seperti yang sudah dijelaskan di awal, bahwa terdapat tak terhingga banyaknya jalur untuk \( (x,y) \to (a,b) \). Kita akan mencoba jalur lain yang juga sering digunakan. Dalam kasus ini, kita akan bergerak sepanjang jalur y = x. Untuk melakukan ini, kita akan menggantikan semua nilai y dengan x dan kemudian membiarkan x mendekati nol. Kita peroleh berikut ini.

Jadi, kita peroleh nilai yang berbeda dengan dua jalur sebelumnya dan ini berarti bahwa limit tersebut tidak mungkin ada.
Contoh 6:
Hitunglah limit berikut jika ada:
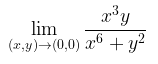
Penyelesaian:
Fungsi tidak terdefinisi pada titik asal dan juga kita tidak bisa melakukan pemfaktoran di sini. Jadi, kita akan coba mengambil beberapa jalur untuk melihat apakah akan diperoleh nilai limit yang berbeda. Jika ya, maka limit tidak ada.
Pertama, kita akan menggunakan jalur y = x. Kita peroleh berikut ini.

Sekarang, mari kita coba jalur yang lain yakni jalur \( y=x^3 \). Sepanjang jalur ini, kita peroleh limit berikut.
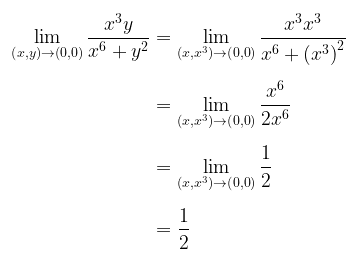
Karena kedua jalur menghasilkan nilai limit yang berlainan, maka ini berarti limit tersebut tidak mungkin ada.
Sumber:
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
When you judge another, you do not define them; you define yourself.
Wayne Dyer
