www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Integral Lipat Dua › Integral Lipat Dua Atas Daerah Bukan Persegi Panjang - Materi, Contoh Soal dan Pembahasan
Integral Lipat
Integral Lipat Dua Atas Daerah Bukan Persegi Panjang - Materi, Contoh Soal dan Pembahasan
Batas-batas integral lipat dua dapat berupa suatu daerah persegi panjang dan daerah bukan persegi panjang. Di sini, kita akan mempelajari integral lipat dua dengan batas-batas berupa daerah bukan persegi panjang.
Pada artikel sebelumnya, kita telah membahas integral lipat dua untuk daerah berupa persegi panjang. Pada artikel ini, kita lanjutkan integral lipat dua untuk daerah yang bukan persegi panjang.
Sekarang perhatikan suatu daerah \(S\) tertutup dan terbatas pada suatu bidang seperti terlihat Gambar 1 di bawah. Daerah \(S\) dikelilingi oleh suatu persegi panjang \(R\) dengan sisi-sisinya sejajar sumbu-sumbu koordinat (Gambar 1).
Andaikan terdapat suatu fungsi dua peubah \(f(x,y)\) yang terdefinisi pada S dan misalkan \(f(x,y)=0\) pada bagian \(R\) di luar \(S\) (Gambar 2), maka kita katakan bahwa \(f\) dapat diintegralkan pada \(S\) jika ia dapat diintegralkan pada \(R\) dan tuliskan sebagai berikut:
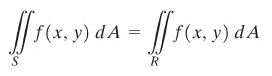
Gambar 1 (Kiri) dan 2 (Kanan)
Integral Lipat Dua atas Himpunan-Himpunan Umum
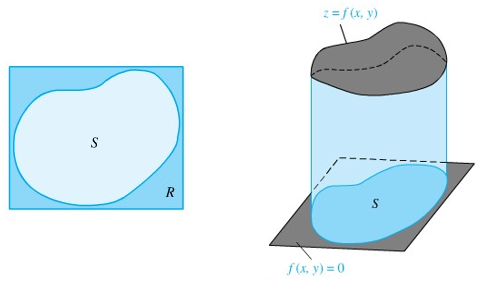
Himpunan atau daerah pengintegralan lipat dua dengan batas-batas melengkung dapat menjadi sangat rumit. Di sini, kita cukup meninjau apa yang disebut himpunan \(x\) sederhana dan himpunan \(y\) sederhana. Suatu himpunan \(S\) adalah \(y\) sederhana (Gambar 3) jika terdapat fungsi-fungsi kontinu \(ϕ_1\) dan \(ϕ_2\) pada \([a,b]\) sedemikian sehingga

Suatu himpunan \(S\) adalah \(x\) sederhana (Gambar 4) jika terdapat fungsi-fungsi kontinu \(ψ_1\) dan \(ψ_2\) pada \([c, d]\) sedemikian sehingga
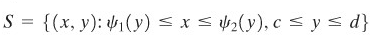

Gambar 3 (Kiri) dan 4 (Kanan)
Perhatikan bahwa setiap garis tegak memotong suatu himpunan \(y\) sederhana dalam satu ruas garis. Hal yang sama berlaku untuk himpunan \(x\) sederhana dengan garis-garis mendatar. Gambar 5 memperlihatkan suatu himpunan yang bukan \(x\) sederhana maupun \(y\) sederhana.

Gambar 5 (Kiri) dan 6 (Kanan)
Sekarang andaikan kita ingin menghitung integral lipat dua dari suatu fungsi \(f(x,y)\) atau suatu himpunan \(S\) yang \(y\) sederhana. Kita lingkungi \(S\) dalam suatu persegi panjang \(R\) (Gambar 6) dan membuat \(f(x,y)=0\) di luar \(S\). Maka

Secara ringkas,

Dalam integral sebelah dalam, \(x\) dipertahankan tetap; jadi pengintegralan itu adalah sepanjang garis tebal dari Gambar 6. Pengintegralan ini menghasilkan luas \(A(x)\) dari penampang yang diperlihatkan pada Gambar 7 di bawah. Kemudian, \(A(x)\) diintegralkan mulai dari \(a\) sampai \(b\).
Jika himpunan \(S\) adalah \(x\) sederhana (Gambar 4), penalaran serupa akan menghasilkan rumus berikut:


Gambar 7 (Kiri) dan 8 (Kanan)
Jika himpunan S bukan \(x\) sederhana maupun \(y\) sederhana (Gambar 5), biasanya ia dapat dipandang sebagai suatu gabungan potongan-potongan yang berupa himpunan x sederhana atau y sederhana. Sebagai contoh, annulus dalam Gambar 8 merupakan gabungan dua himpunan \(y\) sederhana yaitu \(S_1\) dan \(S_2\). Integral pada potongan-potongan ini dapat dihitung dan ditambahkan bersama untuk memperoleh integral atas \(S\).
Contoh-Contoh Soal
Contoh 1:
Hitunglah integral lipat berikut:

Penyelesaian:
Pertama kita melakukan pengintegralan sebelah dalam terhadap \(y\), yang secara sementara memikirkan \(x\) sebagai suatu konstanta (Lihat Gambar 9). Kita peroleh:
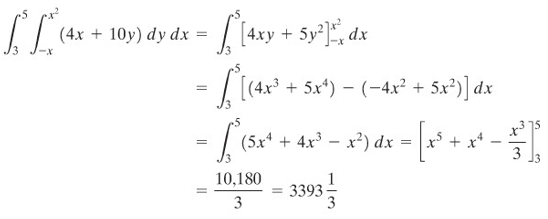

Gambar 9
Contoh 2:
Hitunglah integral lipat berikut:

Penyelesaian:
Daerah integrasi ditunjukkan dalam Gambar 10.


Gambar 10
Contoh 3:
Gunakan pengintegralan lipat-dua untuk menentukan volume bidang empat (‘tetrahedron’) yang dibatasi oleh bidang-bidang koordinat dan bidang \(3x+6y+4z-12=0\).
Penyelesaian:
Nyatakan daerah segitiga di bidang yang membentuk alas bidang empat sebagai S (Gambar 11). Kita mencari volume benda pejal di bawah permukaan \(z=3/4 (4-x-2y)\) dan di atas daerah S.
Bidang yang diberikan memotong bidang \(xy\) di garis \(x+2y-4=0\), yang ruasnya termasuk batas dari S. Karena persamaan ini dapat dituliskan sebagai \(y=2-x/2\) dan \(x=4-2y\), \(S\) dapat dipikirkan sebagai himpunan \(y\) sederhana

atau sebagai himpunan \(x\) sederhana


Gambar 11
Di sini, kita akan memperlakukan \(S\) sebagai suatu himpunan \(y\) sederhana; hasil akhir akan sama jika kita memberlakukan \(S\) sebagai himpunan \(x\) sederhana.
Volume \(V\) dari benda pejal yaitu:

Dalam menuliskan ini sebagai sebuah integral lipat, kita tetapkan \(x\) dan integralkan sepanjang garis (Gambar 11) mulai dari \(y=0\) ke \(y=2-x/2\), kemudian integralkan hasil tersebut dari \(x = 0\) ke \(x = 4\). Jadi,

Contoh 4:
Tentukan volume benda pejal di oktan pertama \((x≥0,y≥0,z≥0)\) yang dibatasi oleh paraboloid bundar \(z=x^2+y^2\), tabung \(x^2+y^2=4\), dan bidang-bidang koordinat (Gambar 12).
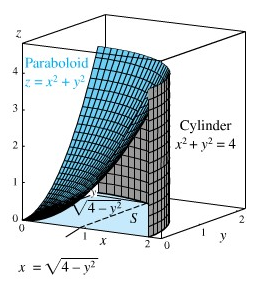
Gambar 12
Penyelesaian:
Daerah \(S\) dikuadran pertama dari bidang \(xy\) dibatasi oleh seperempat lingkaran \(x^2+y^2=4\) dan garis \(x=0\) dan \(y=0\). Walaupun \(S\) dapat dipandang sebagai suatu daerah \(y\) sederhana atau x sederhana, kita akan memperlakukan \(S\) sebagai daerah x sederhana dan menuliskan kurva-kurva batasnya sebagai \(x=\sqrt{4-y^2}, \ x=0\), dan \(y=0\). Jadi,
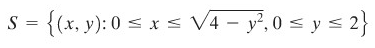

Gambar 13.
Gambar 13 menunjukkan daerah \(S\) dalam bidang-\(xy\). Sasaran kita adalah menghitung

dengan memakai integral lipat. Kali ini, pertama kita tetapkan y dan integralkan sepanjang suatu garis (Gambar 13) mulai dari \(x = 0\) ke \(x=\sqrt{4-y^2}\), kemudian integralkan hasilnya mulai dari \(y=0\) ke \(y=2\).

Dengan mensubstitusi trigonometri \(y=2 sin θ\), integral yang belakangan dapat diulang tulis sebagai

Contoh 5:
Dengan cara perubahan urutan pengintegralan, hitung
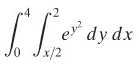
Penyelesaian:
Integral yang sebelah dalam tak dapat dihitung sebagaimana adanya karena \(e^{y^2}\) tidak mempunyai anti-turunan elementer. Tetapi, kita kenali bahwa integral lipat yang diberikan adalah sama terhadap

dengan \(S={(x,y):x/2≤y≤2,0≤x≤4}\) (lihat Gambar 14). Jika integral lipat-dua ini kita tuliskan sebagai suatu integral lipat dengan pengintegralan \(x\) yang pertama dilakukan, kita peroleh
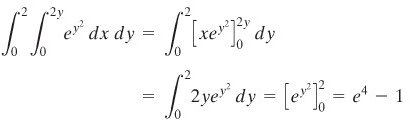

Gambar 14
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Kalkulus dan Geometri Analitis, ed 5. Terjemahan Susila, I Nyoman, dkk. Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
The future depends on what we do in the present.
Mahatma Gandhi
