Uji Deret-P - Materi, Contoh Soal dan Pembahasan

Kalkulus II » Uji Kekonvergenan Deret Tak Hingga › Uji Deret-P - Materi, Contoh Soal dan Pembahasan

Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Deret

Uji Deret-P - Materi, Contoh Soal dan Pembahasan

Salah satu uji kekonvergenan yang penting dikenal dengan uji deret-p (p-series test). Deret akan konvergen jika p > 1 dan divergen untuk 0 < p ≤ 1. Khusus untuk p = 1, maka deret yang dihasilkan disebut deret harmonik yang merupakan deret yang divergen.

Salah satu uji kekonvergenan yang penting dikenal dengan uji deret-p (p-series test). Uji ini merupakan kasus khusus uji integral untuk deret yang positif. Perhatikan deret berikut ini

Deret di atas disebut deret-p. Secara umum, deret-p mempunyai bentuk yang dapat dinyatakan sebagai berikut.

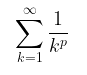
Deret tersebut akan konvergen jika \(p > 1\) dan divergen untuk \(0 < p \leq 1\). Khusus untuk \(p = 1\), deret yang dihasilkan disebut deret harmonik yang merupakan deret yang divergen. Untuk lebih tepatnya, kita nyatakan dalam teorema berikut ini.

Uji Deret-P

Misalkan terdapat deret berikut:

\begin{aligned} \sum_{k=1}^\infty \ \frac{1}{k^p} = 1 + \frac{1}{2^p} + \frac{1}{3^p} + \frac{1}{4^p} + \cdots \end{aligned}

Deret di atas disebut deret-p dan konvergen jika \(p > 1\) dan divergen untuk \(0 < p \leq 1\).

Contoh 1:

Tentukan apakah deret \( \displaystyle{\sum_{k=1}^\infty} \frac{1}{\sqrt[3]{k^2}} \) konvergen atau divergen.

Pembahasan:

Perhatikan bahwa

\[ \sum_{k=1}^\infty \frac{1}{\sqrt[3]{k^2}} = \sum_{k=1}^\infty \frac{1}{k^{2/3}} \]

Karena \(p = \frac{2}{3} < 1\), maka berdasarkan uji deret-p, deret dalam soal ini adalah divergen.

Contoh 2:

Tentukan apakah deret \(\displaystyle{\sum_{k=1}^\infty} k^{-4/3} \) konvergen atau divergen.

Pembahasan:

Perhatikan bahwa

\[ \sum_{k=1}^\infty k^{-4/3} = \sum_{k=1}^\infty \frac{1}{k^{4/3}} \]

Karena \(p = \frac{4}{3} > 1\), maka berdasarkan uji deret-p, deret dalam soal ini adalah konvergen.

Sumber:

Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

KALKULUS II

Kalkulus II » Uji Kekonvergenan Deret Tak Hingga › Uji Deret-P - Materi, Contoh Soal dan Pembahasan

Deret