www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Uji Kekonvergenan Deret Tak Hingga › Uji Deret Ganti Tanda - Materi, Contoh Soal dan Pembahasan
Deret
Uji Deret Ganti Tanda - Materi, Contoh Soal dan Pembahasan
Deret ganti-tanda adalah deret yang suku-sukunya berganti-ganti tandanya (alternating series). Pada artikel ini, kita akan menentukan kekonvergenan deret ganti-tanda.
Kita telah membahas deret-deret yang suku-sukunya tak negatif dalam beberapa artikel sebelumnya. Sekarang persyaratan tak negatif ini kita hapus, sehingga dalam suatu deret suku-sukunya dapat negatif. Khususnya kita memperlihatkan deret-deret yang suku-sukunya berganti-ganti tandanya (alternating series) – yakni, deret yang bentuknya

dengan \(a_n>0\) untuk semua \(n\). Contoh penting adalah deret harmonik ganti tanda

Kita tahu bahwa deret harmonik itu divergen; tapi kita akan melihat dalam waktu singkat bahwa deret harmonik ganti tanda itu konvergen.
Teorema A: Uji Deret Ganti-Tanda.
Andaikan

suatu deret ganti-tanda dengan \(a_n>a_{n+1}>0\). Apabila \(\displaystyle{\lim_{n\to\infty}} a_n = 0\), maka deret konvergen. Selain itu, kesalahan (error) yang dibuat apabila jumlah \(S\) diaproksimasi dengan jumlah \(n\) suku pertama \(S_n\), tidak akan melebihi \(a_{n+1}\).
Contoh 1:
Buktikan bahwa deret harmonik yang ganti tanda

adalah konvergen. Berapa sukukah harus kita ambil agar selisih antara jumlah deret \(S\) dan jumlah parsial \(S_n\) tidak melebihi \(0,01\).
Penyelesaian:
Deret harmonik yang diketahui memenuhi syarat-syarat Teorema A. Jadi deret tersebut konvergen. Kita menginginkan agar \(|S-Sn|≤0,01\). Ini dapat terpenuhi apabila \(a_{n+1}≤0,01\). Karena \(a_{n+1}=1/(n+1)\), maka haruslah \(1/(n+1)≤0,01\). Ketaksamaan ini dipenuhi apabila \(n≥99\). Jadi kita harus mengambil 99 suku untuk menghampiri \(S\) dengan ketelitian yang diinginkan. Dengan uraian tersebut dapat dilihat betapa lambatnya kekonvergenan deret tersebut.
Contoh 2:
Buktikan bahwa deret
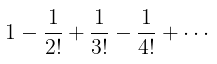
adalah konvergen. Hitunglah \(S_5\) dan perkirakanlah kesalahan (galat) yang kita buat apabila jumlah deret itu kita hampiri dengan jumlah parsial tersebut.
Penyelesaian:
Persyaratan Teorema A dipenuhi oleh deret yang diketahui, jadi deret konvergen.

Contoh 3:
Buktikan bahwa \(\displaystyle{\sum_{n=1}^\infty} (-1)^{n+1} \frac{n^2}{2^n} \) konvergen.
Penyelesaian:
Untuk dapat menggambarkan deret itu kita menuliskan beberapa suku permulaan:
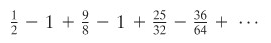
Deret itu berganti tanda dan \(\displaystyle{\lim_{n\to\infty}} \frac{n^2}{2^n} = 0 \) (Kaidah I’Hopital), tetapi suku-suku deret tidak menurun dari permulaan. Suku-suku mulai menurun pada suku ketiga; ini sudah cukup, karena kekonvergenan atau kedivergenan deret tidak dipengaruhi oleh suku-suku permulaan. Untuk membuktikan bahwa barisan \(\{n^2/2^n\}\) menurun mulai dari suku ketiga, perhatikan fungsinya
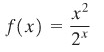
Perhatikan bahwa jika \(x≥3\), turunan

Jadi, \(f\) menurun pada \([3,∞)\), dan demikian pula \(\{n^2/2^n\}\) untuk \(n≥3\).
Sumber:
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
Being deeply loved by someone gives you strength, while loving someone deeply gives you courage.
Lao Tzu
