www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
KALKULUS II
Kalkulus II
Kalkulus II » Turunan Fungsi Peubah Banyak › Turunan Parsial Fungsi Peubah Banyak - Materi, Contoh Soal dan Pembahasan
Turunan Fungsi Peubah Banyak
Turunan Parsial Fungsi Peubah Banyak - Materi, Contoh Soal dan Pembahasan
Turunan parsial sebuah fungsi peubah banyak adalah turunannya terhadap salah satu peubah (variabel) dengan peubah lainnya dipertahankan konstan.
Turunan parsial sebuah fungsi peubah banyak adalah turunannya terhadap salah satu peubah (variabel) dengan peubah lainnya dipertahankan konstan.
Sebagai contoh, misalkan \(f\) adalah suatu fungsi dua peubah \(x\) dan \(y\). Jika \(y\) ditahan agar konstan, misalnya \(y=y_0\), maka \(f(x,y_0)\) menjadi fungsi satu peubah \(x\). Turunannya di \(x=x_0\) disebut turunan parsial \(f\) terhadap \(x\) di \((x_0,y_0)\) dan dinyatakan sebagai \(f_x(x_0,y_0)\).
Jadi, kita dapat menuliskan sebagai berikut.
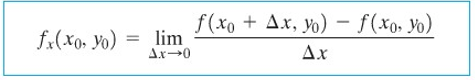
Demikian pula, turunan parsial \(f\) terhadap \(y\) di \((x_0,y_0)\) dinyatakan oleh \(f_y (x_0,y_0)\) dan dituliskan sebagai
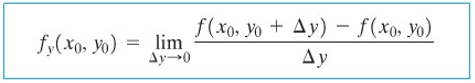
Menghitung \(f_x(x_0,y_0)\) dan \(f_y(x_0,y_0)\) secara langsung dari definisi di atas tidak hanya memakan waktu, tetapi juga membosankan. Oleh karena itu, kita tidak akan banyak menggunakan rumus pada definisi di atas, melainkan kita akan mencari \(f_x(x,y)\) dan \(f_y(x,y)\) dengan menggunakan aturan baku untuk turunan; kemudian kita mensubstitusikan \(x=x_0\) dan \(y=y_0\).
Contoh 1:
Carilah \(f_x(1,2)\) dan \(f_y(1,2)\) jika \(f(x,y)=x^2 y+3y^3\).
Penyelesaian:
Untuk mencari \(f_x(x,y)\) kita anggap \(y\) sebagai konstanta dan kita diferensialkan fungsi ini terhadap x. Kita peroleh

Jadi,

Demikian pula,
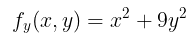
Sehingga,

Jika \(z=f(x,y)\), kita gunakan cara penulisan lain untuk menyatakan turunan parsial, yakni

Lambang \(∂\) adalah lambang khas dalam matematika dan disebut tanda turunan parsial.
Contoh 2:
Jika \(z=x^2 \sin{(xy^2)}\), carilah \(∂z/∂x\) dan \(∂z/∂y\).
Penyelesaian:
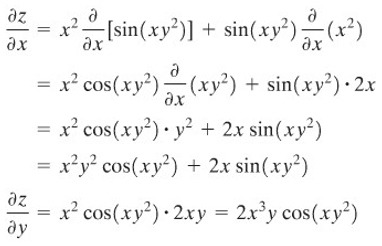
Untuk mendapatkan gambaran geometris terkait turunan parsial khususnya untuk fungsi dua peubah, amatilah permukaan yang persamaannya \(z=f(x,y)\) pada Gambar 1 di bawah. Bidang \(y=y_0\) memotong permukaan ini pada kurva bidang QPR (Gambar 1 sebelah kiri) dan nilai dari \(f_x(x_0,y_0)\) adalah kemiringan garis singgung pada kurva ini di \(P(x_0,y_0,f(x_0,y_0)\)).
Serupa dengan itu, bidang \(x=x_0\) memotong permukaan pada kurva bidang LPM (Gambar 1 sebelah kanan) dan \(f_y(x_0,y_0)\) adalah kemiringan garis singgung pada lengkungan ini di titik P.

Gambar 1.
Turunan Parsial Tingkat Tnggi
Secara umum, karena turunan parsial suatu \(x\) dan \(y\) adalah fungsi lain dari dua peubah yang sama ini, turunan tersebut dapat diturunkan secara parsial terhadap \(x\) atau \(y\) untuk memperoleh empat buah turunan parsial kedua fungsi \(f\):
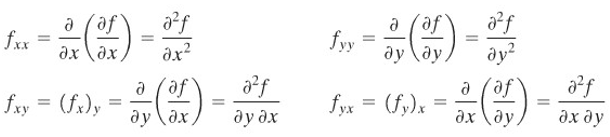
Contoh 3:
Cari keempat turunan parsial kedua dari

Penyelesaian:

Perhatikan bahwa \(f_{xy}=f_{yx}\).
Turunan parsial tingkat tiga dan lebih tinggi didefinisikan dengan cara yang sama dan cara penulisannya pun serupa. Jadi, jika \(f\) suatu fungsi dua peubah \(x\) dan \(y\), turunan parsial-ketiga \(f\) yang diperoleh dengan menurunkan \(f\) secara parsial, pertama kali terhadap \(x\) dan kemudian dua kali terhadap \(y\), akan ditunjukkan oleh

Secara keseluruhan akan terdapat delapan buah turunan parsial ketiga.
Peubah lebih dari dua
Andaikan \(f\) suatu fungsi tiga peubah \(x, \ y\), dan \(z\). Turunan parsial \(f\) terhadap \(x\) di \((x,y,z)\) dinyatakan oleh \(f_x (x,y,z)\) atau \(∂f(x,y,z)/∂x\) dan didefinisikan oleh

Jadi \(f_x (x,y,z)\) boleh diperoleh dengan memperlakukan \(y\) dan \(z\) sebagai konstanta dan menurunakan terhadap x. Turunan parsial terhadap \(y\) dan \(z\) didefinisikan dengan cara yang serupa.
Contoh 4:
Jika \(f(x,y,z)=xy+2yz+3zx\), carilah \(f_x,f_y,\) dan \(f_z\).
Penyelesaian:
Untuk memperoleh \(f_x\), kita pandang \(y\) dan \(z\) sebagai konstanta dan turunkan terhadap peubah \(x\). Jadi,
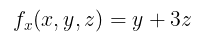
Untuk mencari \(f_y\), kita anggap \(x\) dan \(z\) sebagai konstanta dan turunkan terhadap peubah \(y\);

Serupa halnya,
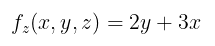
Contoh 5:
Jika \(T(w,x,y,z)=ze^{w^2+x^2+y^2}\), carilah semua turunan parsial pertama dan \( \displaystyle{\frac{∂^2 T}{∂w∂x}, \, \frac{∂^2 T}{∂x∂w}} ,\) dan \( \displaystyle{\frac{∂^2 T}{∂z^2}} \).
Penyelesaian:
Empat turunan parsial adalah

Turunan parsial yang lain adalah
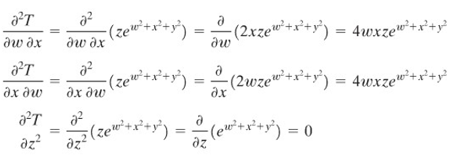
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.
Artikel Terkait
The real opportunity for success lies within the person and not in the job.
Zig Ziglar
